Change in Internal Energy
- When a gas is compressed, there is work done to move the particles closer together, increasing the pressure.
- This increases the potential energy of the particles due to intermolecular attractive forces.
- The energy transfer results in an increase in temperature during compression, which increases the kinetic energy of the particles.
- Therefore, mechanical energy will be transferred to thermal energy when a gas is compressed.
- When a piston compresses the gas rapidly, the amount of work done is the same but the rate of energy transfer is greater so the temperature will rise more rapidly than if the compression is done slowly.
- This also means the power of the work done on the gas is greater.
- We can describe this phenomenon with the formula:
- W = PΔV
- Where W is work in joules
- P is pressure in pascals, which remains constant
- ΔV is the change in volume, in meters cubed.
- W = PΔV
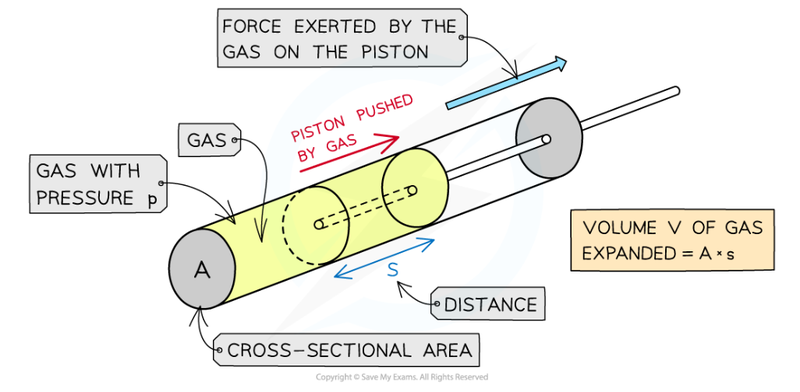
- The formula is derived from the formula for work, W = Fs.

- If we decrease the volume by compression, the surrounding is doing work on the gas.
- However, if the volume is increased through expansion, then the gas is doing work on the surroundings.
- Work done can also be calculated as the area under a pressure to volume graph.
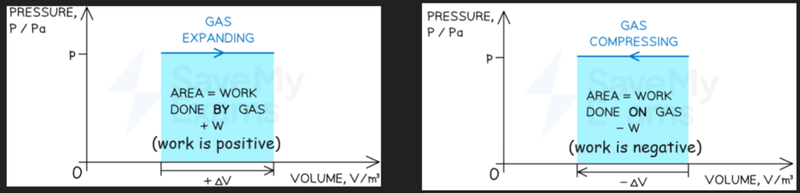
- Whether work done is positive or negative depends on whether the gas is being compressed or expanded.
- Compression means work done is negative.
- Expansion means work done is positive.
- However, keep in mind that if you are calculating this directly from a graph, work done will always appear positive.
- In this case, you have to know whether the gas is being expanded or compressed.
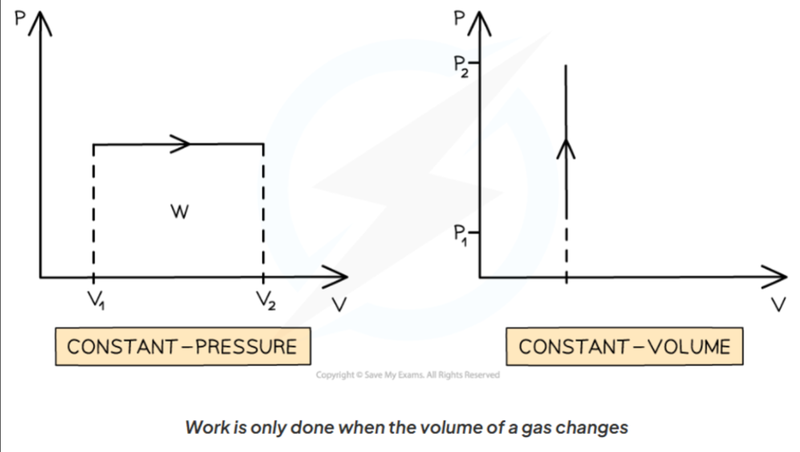
- Keep in mind that this formula only works for constant pressure.
- If volume is constant, then no work is done.
- Lastly, when using this equation, it is important to remember what values are positive and what values are negative.

Sources