What are Vectors?
- In physics there are both scalar and vector quantities.
- Scalar quantities consist of only a magnitude and are independent of direction.
- Think of for example mass and time. An object can't have a mass in any sort of direction, and thus it is scalar.
- Scalar quantities can only be positive, as they are not based on direction.
- Other types of units need to have a direction to be fully defined.
- These types of units are called vectors.
- Vectors have both magnitude and direction.
- This means that the unit is directed towards a certain point. For example an object could be moving with a velocity of 15 m/s to the east.
- Vector quantities can be either positive or negative, depending on their direction.
- In a chosen direction, a vector quantity is positive, and in the opposite direction of the chosen one it is negative.
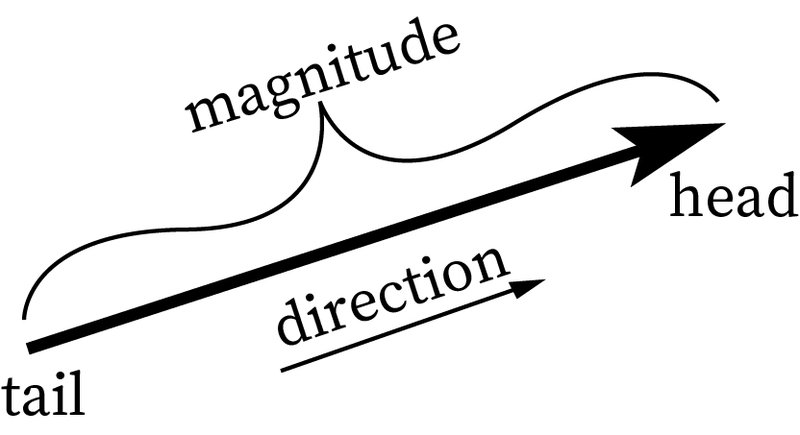
Drawing Vectors
- Vectors are drawn as arrows.
- The length of the arrow is its magnitude, and the direction the head points is the direction the unit is pointed.
- Magnitude is always proportional. If you were to double the length of the arrow, you would have doubled
Solving Vectors
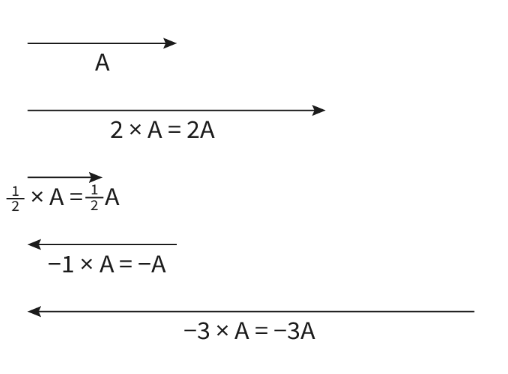
Multiplying Vectors by Scalars
- A vector can be multiplied by a scalar in order to change its magnitude.
- Multiplying vectors changes the length of the vector.
- Values larger than one increase the length of the vector and values less than one will decrease the length of the vector.
- Multiplying a vector by a scalar with a value of 0 makes the vector not exist. Imagine for example, how much distance a person could walk in 0 seconds?
Adding Vectors
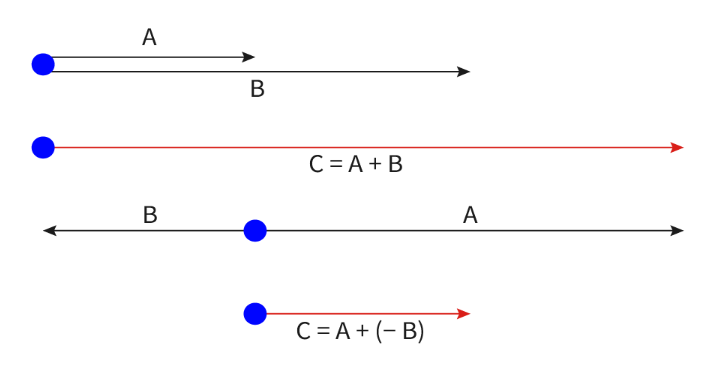
- Vectors can also be added or subtracted from one another as long as they represent the same physical quantity, depending on their direction.
- If two vectors of the same quantity face the same direction, meaning they are parallel, then their magnitudes can directly be added to one another.
- If the vectors face the opposite direction however, their magnitudes are subtracted from one another instead.
- Remember to always keep vectors proportional to one another. If vector B has double the magnitude of vector A, it should be exactly twice as long.
- If the vectors aren't aligned then different methods can be used to add them together.
- For example in a situation where at least some angles are known, trigonometry can be used to align the vectors and thus add them together.
- However, if you are not given such information then you can simply draw the vectors instead.
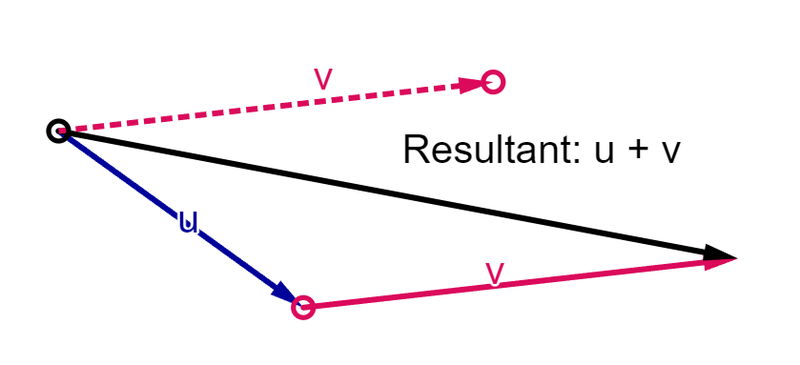
- Vectors can be moved around freely as long as their magnitude and direction stays the same.
- Thus you can bring two vectors end to head to tail and add them together by drawing a line that stretches from the tail of the first vector and to the head of the last vector.
- If drawing the line forms a right triangle, then the Pythagorean theorem can be used to find the magnitude of the sum vector.
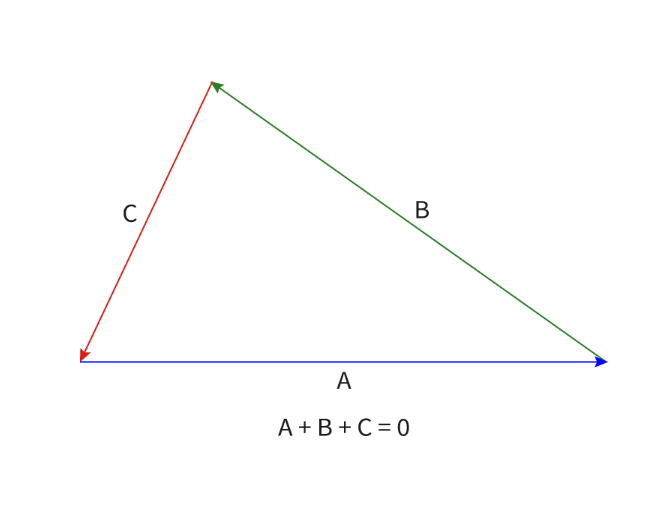
- If the head of the last vector is at the tail of the first vector, then the value cancels itself out and it is zero.
- For example, in the image below, vector v can be moved from its original position to the head of vector u. Then they can be added together by drawing a line from the tail of u to the head of v.
- In the image below, the vector ends where it started and thus has a value of 0.
- Solving vectors usually requires them to be split into their components.
- Trigonometry can be used to find the values of a vector along the x and y axis for example, which can then be added or subtracted from other vector components to find the sum of two vectors.
Examples of Vector and Scalar Quantities
Vector
- Displacement
- Velocity
- Acceleration
- Momentum
- Force
- Weight
Scalar
- Distance
- Speed
- Tangential acceleration
- Energy
- Work
- Power
- Time
- Mass
- Volume
- Density
- Length
- Temperature
Determining Vectors
- Whether a quantity is a vector or scalar can be determined based on the units it is composed of.
- As vectors can have negative signs to indicate direction, the way they are determined is similar to how the signs of products of positive and negative numbers are determined.
- If a vector quantity is multiplied or divided by a vector, then any negative sign would cancel out, and the indication of direction would be lost.
- Thus a vector multiplied or divided by a vector must be scalar.
- If a vector quantity is multiplied or divided by a scalar, the sign does not change as scalar quantities are always positive.
- This means the quantity can still indicate direction, and thus the resulting quantity is vector as well.
- If a scalar is multiplied or divided by a scalar, then the final quantity is still scalar, as neither quantities could show direction to begin with.
Sources
https://www.bartleby.com/subject/math/calculus/concepts/vectors
Kognity - Physics Book