Thermodynamic Processes

Change in Internal Energy

• We know that the kinetic energy of a gas is proportional to the absolute temperature of the gas.
• The total kinetic energy of its particles can be given as:

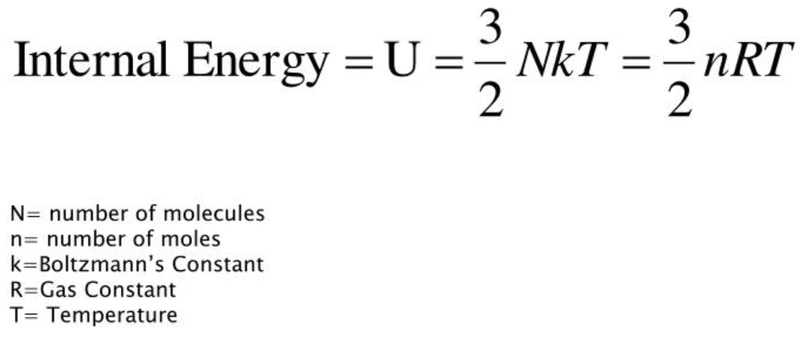
• Remember that in the formula above the gas is considered to have no potential energy between its molecules.
• Since Ideal gases have zero potential energy (due to negligible intermolecular forces), this formula yields the internal energy of an ideal gas.

The First Law of Thermodynamics

• The first law of thermodynamics states that energy is always conserved.

• Here work done by the gas is described by the formula: W = PΔV.

The Four Thermodynamic Processes

• The first law of thermodynamics can be used to describe the four thermodynamic processes.
• These processes are all obtained by keeping one variable fixed and their name alludes to the one being kept constant.
• The processes are:
  • Isovolumetric
    • Volume, V, is kept constant.
    • This is also sometimes called an isochoric process.
  • Isobaric
    • Pressure, P, is kept constant
    • If this one is confusing, think of the unit bars, to measure atmospheric pressure!
  • Isothermal
    • Temperature, T, is kept constant.
  • Adiabatic
    • Thermal energy, Q, is kept constant.
    • This means that ΔU + W = 0

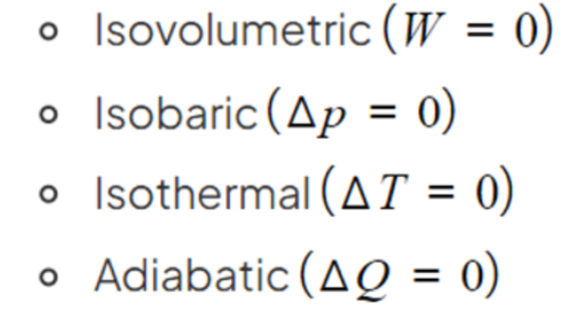
Graphing the Four Thermodynamic Processes

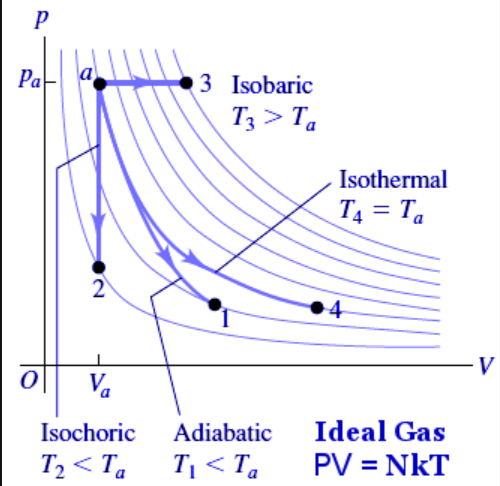
• The different curving lines represent how the gas behaves at different temperatures, while the y-axis is for pressure and the V axis is for volume.
• Isovolumetric/isochoric processes are a vertical movement.
• Isobaric processes are a horizontal movement.
• Isothermal processes are along one of the temperature lines.
• Adiabatic processes shift from one line to another.
  • You can tell an adiabatic process apart from temperature lines due to them having a steeper gradient.

Adiabatic Expansion

• An adiabatic process is one in which there is no exchange of heat between the system and the surroundings.
• If we wanted to increase the volume without adding heat, then the internal energy must go down, resulting in a decrease in temperature.
• Likewise, to decrease the volume without adding any heat, internal energy must increase to that the thermal energy is still equal to zero, resulting in an increase in temperature.

• An adiabatic expansion can be defined by the following equation:

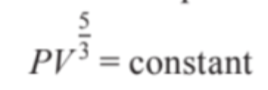
• We can see that P and V^5/3 are inversely proportional to one another.
• Therefore, the shape of the curve of adiabatic expansion can be given as:

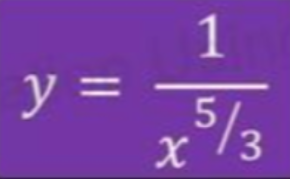
Sources

https://universe-review.ca/R13-09-thermodynamics05.htm