Calculating the Average Temperature of the Earth
- Considering we know the equation for luminosity, and the solar constant, we can calculate the average temperature of the Earth.
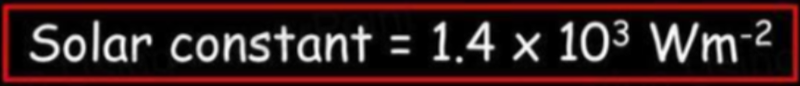
- First we have to consider the total radiation absorbed by the Earth.
- The solar constant gives us the power the Earth receives from the sun per unit area.
- The total power received can be calculated by multiplying the solar constant by the circular surface area of the Earth.
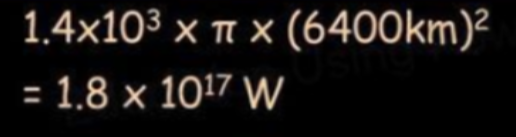
- Then we have to calculate the total power radiated by the Earth.
- Using the luminosity formula, we can reduce things down to just two unknown variables, as we know the Stefan-Boltzmann constant and the distance of the Earth from the Sun.
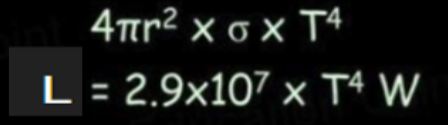
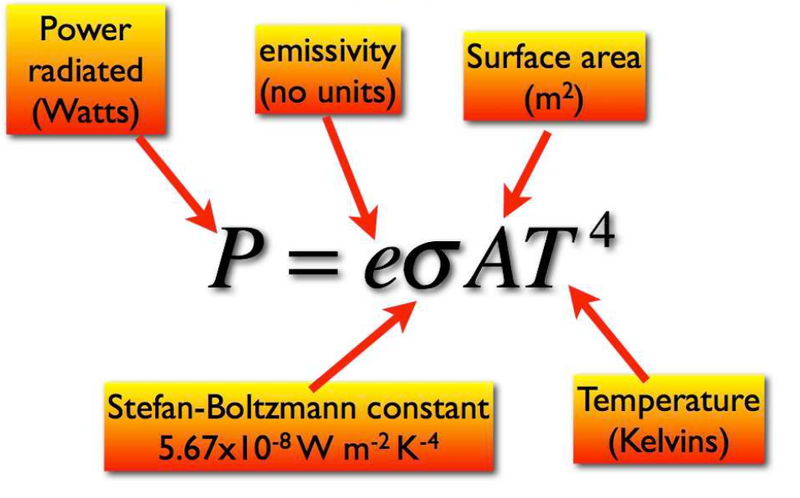
- If we assume the Earth is a black body, all of the power absorbed by the Earth will be radiated by the Earth.
- Thus we can substitute luminosity in the previous equation with the radiation Earth recieves.
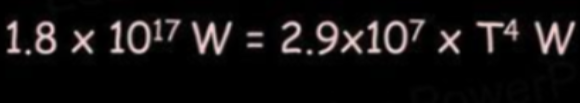
- Now temperature is the only known variable, and we can calculate it to be 280 degrees Kelvin.
- However, this isn't very close to the actual average temperature of the Earth.
Albedo
- For our previous calculation, we had to assume Earth was a black body, when in reality it isn't.
- This is where albedo comes in.
- It is a measure of the average energy reflected off a macroscopic system and itis calculated as:

- Earth's albedo varies daily depending on cloud formations and latitude.
- As albedo is a coefficient, it has no units.
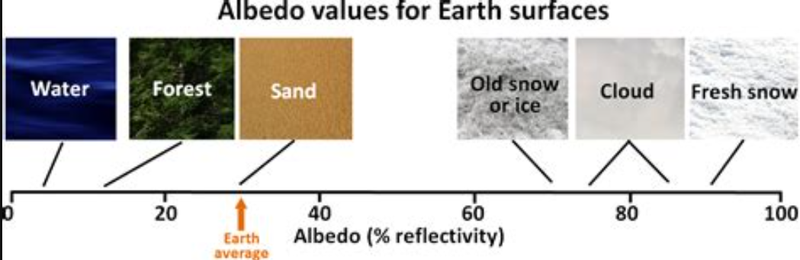
- Earth's albedo varies but it is around 0.3, or 30% on average.
- A perfect black body would have an albedo of 0, as all incident thermal energy would be absorbed.
- An albedo of 1 would represent a surface which scatters all of the incident thermal radiation.
A More Accurate Average Temperature of Earth
- There were several problems with our previously calculated temperature for Earth.
- Firstly, the Earth's albedo is around 0.3 as radiation is absorbed by the ground and scattered by the atmosphere.
- If 30% of the power reaching Earth is scattered, then only 70% must be absorbed.
- That means we should multiply the previous value for power absorbed by 70%, or 0.7.
- Secondly, we assumed that the Earth's emissivity was 1, but in reality it isn't.
- This is because the Earth isn't a black body.
- Additionally, greenhouse gases re-radiate some of the energy back to the Earth, resulting in an emissivity of around 0.6.
- Therefore, we should multiply our value for power radiated by the Earth by 0.6, as only 60% of the power reaching Earth is radiated back.

- The Earth reaches equilibrium temperature when power radiated is equal to power absorbed.
- This means we can equate the two previous calculated variables.

- Temperature is once again the only unknown variable, which we can calculate to find that the Earth's average temperature is actually closer to 292 degrees Kelvin.
Sources
https://cleantechnica.com/2019/02/18/nrel-builds-first-solar-database-for-bifacial-albedo/