Superposition

What is Superposition?

• Superposition is seen when two waves of the same type cross paths while travelling in opposite directions.
• Their displacements add together at every point in space, resulting temporarily in a different wave, until the two waves separate again.

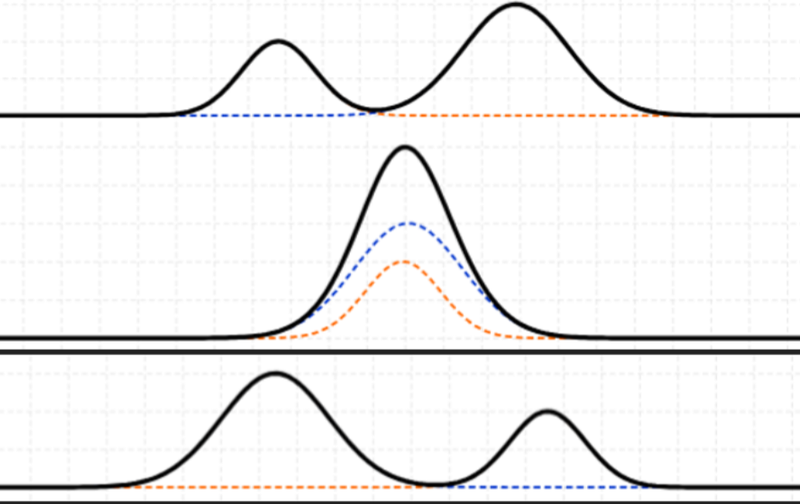
• In the image above, the blue wave is travelling to the right and the orange wave is travelling to the left.
• They then meet, forming a wave of greater amplitude, as both of their positive displacements are added up.
• Then the two waves move away and separate.

Interference

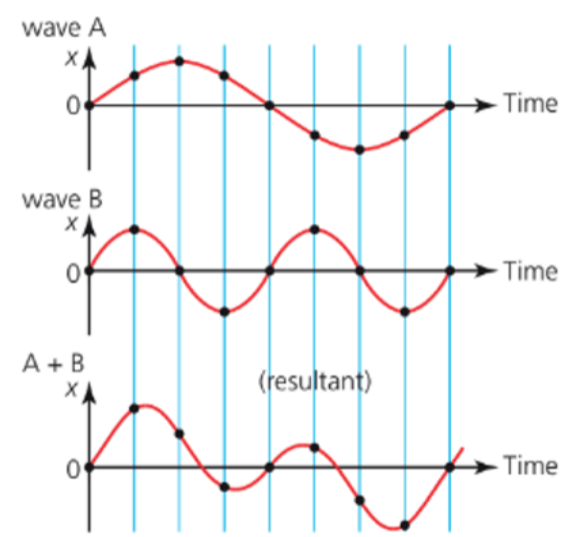
• The superimposition of waves is called interference.
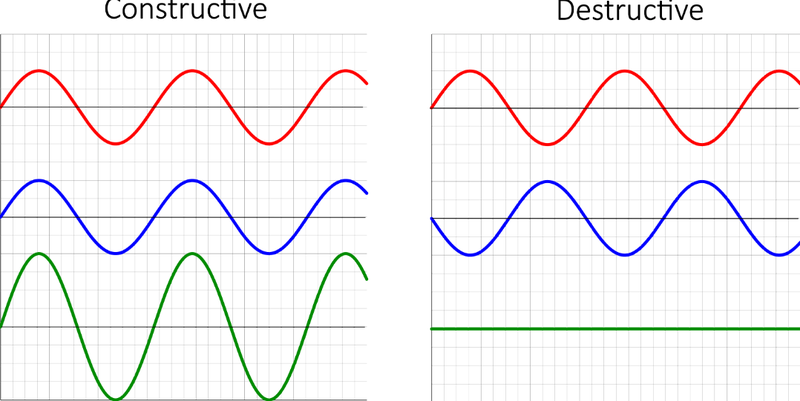
• Interference can either be constructive, or destructive.
• As the displacement of all points are added up, if both of the displacements are positive or negative, then they will add up and lead to a greater superimposed displacement.
• This is constructive interference.

• However, if displacements are of opposite signs, where one is positive and one is negative, then they cancel out and lead to a smaller superimposed displacement.
• This is destructive interference.

• Interference is used by sound-cancelling headphones, which produce a sound wave with a phase difference of π to the sound wave of the noise.
• This results in destructive interference and the noise is cancelled out!

Examples

Destructive Interference of Ropes

Superimposition Patterns

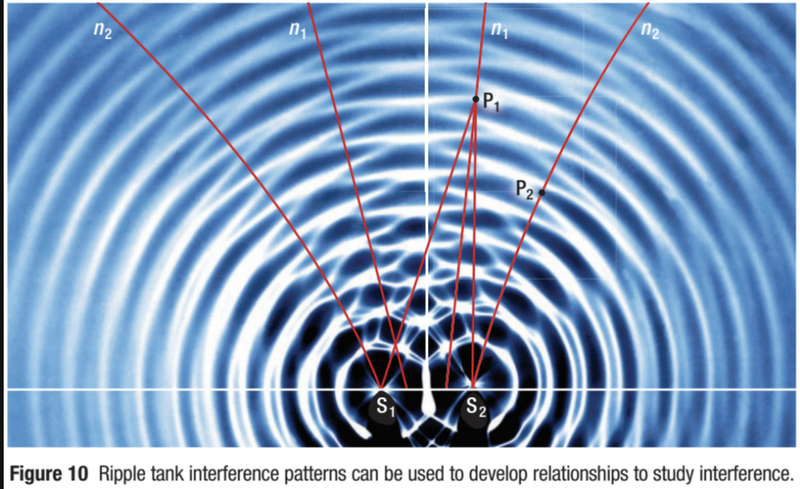
If there are two point sources, stable interference patterns will only occur if the two waves are the same type, coherent and have similar displacements at the point of superimposition.

Coherence

• Two waves are said to be coherent if they have the same frequency and the same constant phase difference.
• Both conditions need to be satisfied for there to be coherence.

Constructive and Deconstructive Interference in Interference Patterns

• If coherent waves have a phase difference of 0, then their crests and troughs line up and there is constructive interference.
• This also occurs if they are shifted by one wavelength, so that their crests and troughs still line up.
• However, if two waves have a phase difference equivalent to half of their wavelength, then the crests of one wave line up with the troughs of the other wave and the troughs of that wave line up with the crests of the other wave.
• This leads to destructive interference.
• From these rules we can determine that:

• Where λ is wavelength and n is an integer number.

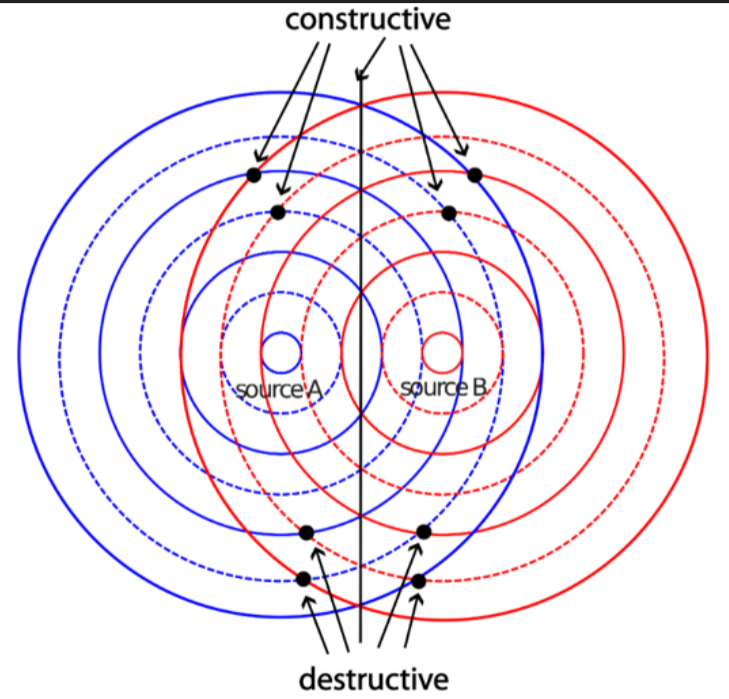
• This can be seen in the above diagram, where dotted lines are troughs and straight lines are crests.
• Where two crests or troughs meet there is constructive interference.
• Where a trough and a crest meet there is destructive interference.

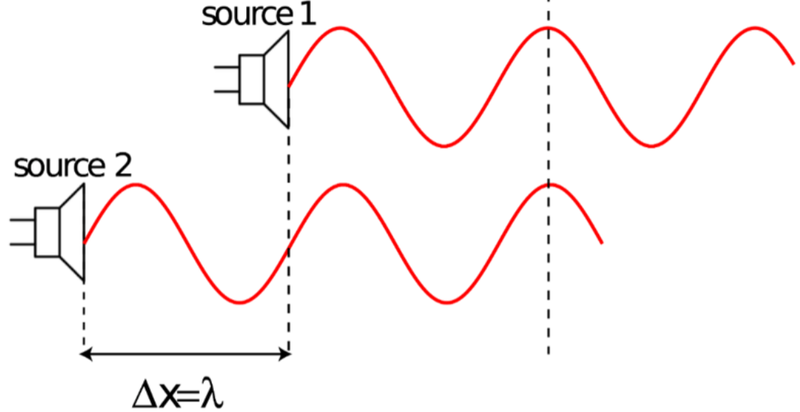
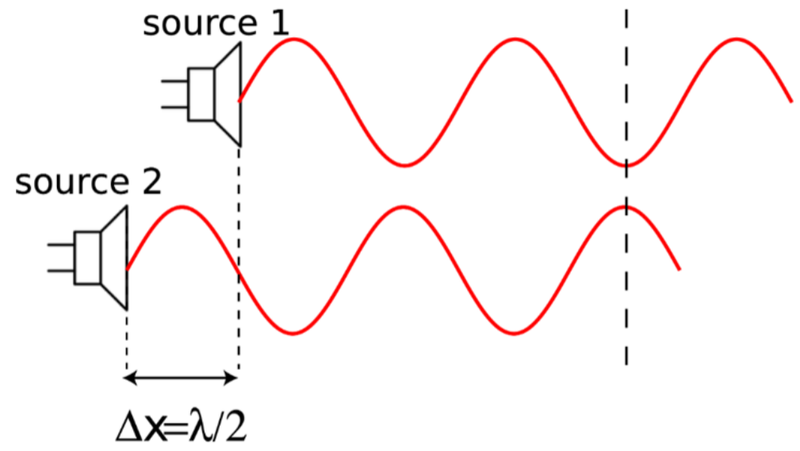
• If the waves sources have identical frequencies then there will be an antinodal line in the exact center of the pattern and an alternating series of nodal and antinodal lines to the left and right of the central antinodal line.
  Each line in the pattern is assigned a name, such as the first antinodal line, and an order number represented by the symbol m.
• Antinodes are points of maximum displacement and nodes are points of zero displacement.

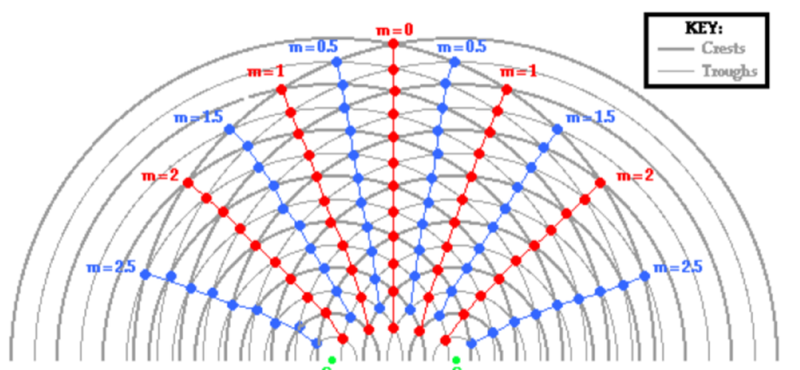
• The red dots represent antinodes and the blue dots represent nodes.
• Thus the red lines are antinodal lines and the blue lines are nodal lines.

Sources

https://ar.inspiredpencil.com/pictures-2023/constructive-interference-of-a-wave