What are Standing Waves?
- Usually waves are described as travelling or progressive waves, indicating that there is a movement of energy as it travels.
- Standing waves, or stationary waves, are waves that do not transmit energy, meaning energy does not travel.
- Standing waves always remain in the same position.
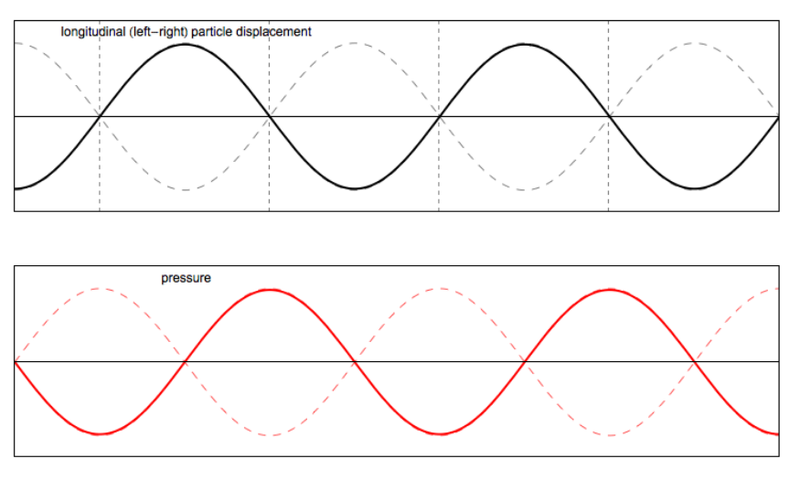
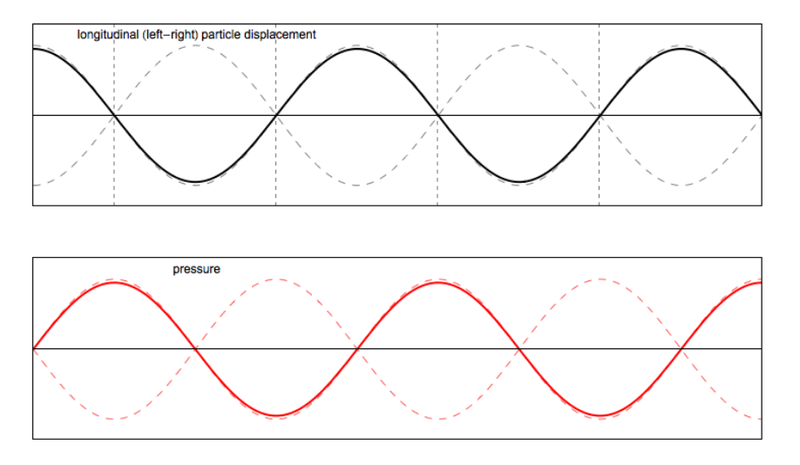
- The standing wave does not move, instead it sort of "flips".
- Standing Waves Animations can be viewed at this link.
- It is possible to set up a standing wave using two travelling waves of equal frequency and wavelength, travelling in the opposite direction.
- The standing wave will have double the amplitude of the two waves (due to superposition) and the same frequency.
- However, as the waves are going the opposite direction, their velocities cancel out, and thus the resulting wave stands still.
- Standing waves usually occur in confined systems in which the same wave is reflected back and forth, which leads to the waves of opposite direction with the same frequency and wavelength needed to create a standing wave.
Comparison to Transverse Waves
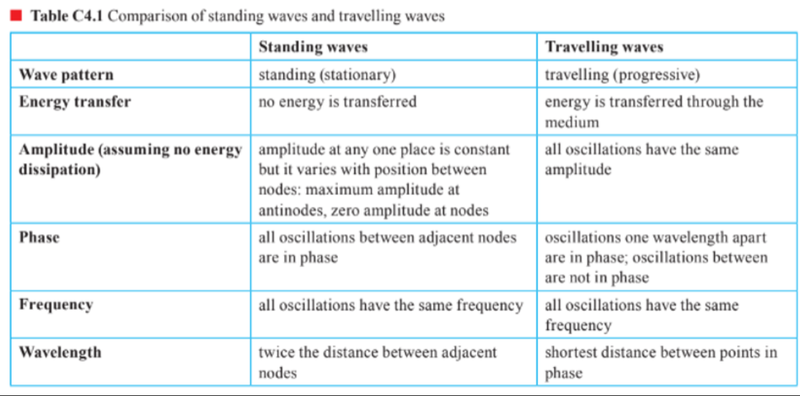
Nodes and Antinodes
- While we went briefly over nodes and antinodes in diffraction patterns, they are most useful in standing waves.
- Nodes are points which do not oscillate, while antinodes are points which do oscillate.
- At nodes the displacement is minimum (often zero).
- At antinodes, the amplitude is the greatest.
- The location of standing waves where the amplitude is always at equilibrium are called nodes, these are the locations where the two counter-propagating waves interfere destructively.
- The distance between two neighboring nodes or two neighboring antinodes is half a wavelength.
- The location where the wave oscillates away from equilibrium with double the amplitude of the original waves are known as antinodes.
- The location where there is no oscillation is a node.
- As the nodes and antinodes alternate, the distance between an adjacent node and and antinode is a quarter of the wavelength.
Standing Wave Graphs
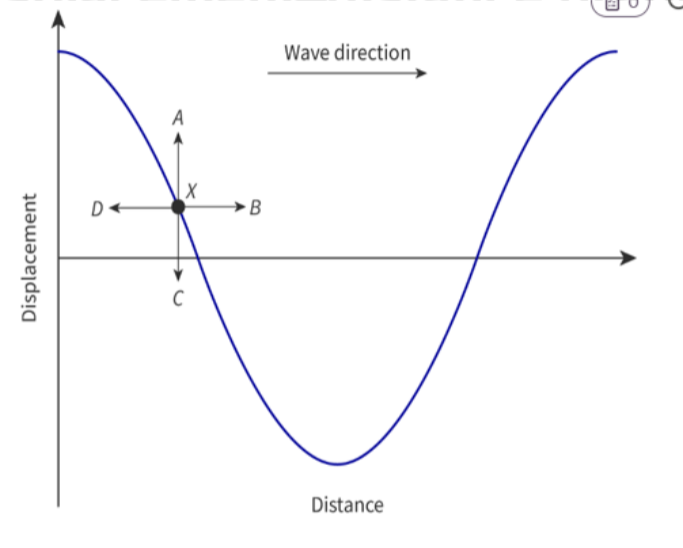
- In the following graph the particle x can only move upwards and downwards, as the graph shows a standing wave.
- Points on a standing wave always move towards the equilibrium position.
- This means that x will move downwards.
- A point below the x-axis would move upwards.
Boundary Conditions
- Boundary conditions are the conditions at the ends of a standing wave system.
- These conditions affect whether there are nodes or antinodes at the end of standing wave.
- A boundary can either be fixed, or open.
- If it is fixed, then the wave is stuck there, and the ending is a node.
- If it is open, then the wave is free to move, and the ending is an antinode.
- The ends of standing waves are always either nodes or antinodes.
Standing Wave Patterns
Standing Wave Patterns in Strings
- Below is a standing wave formed in a string where both ends are fixed.
- As the ending of a standing wave has to be a node, there are are certain amount of waves it can take.
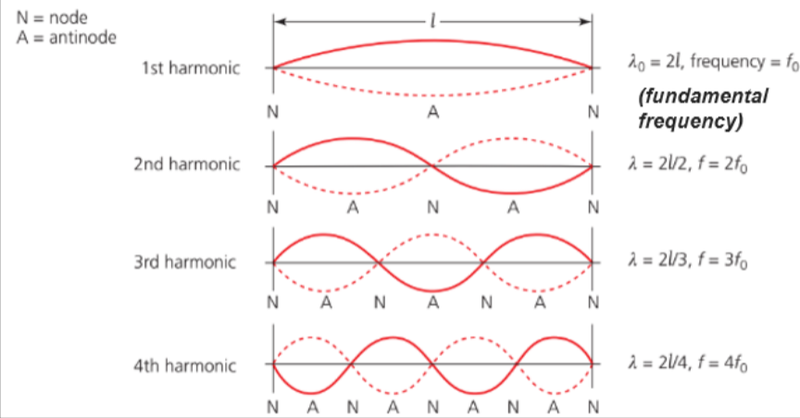
- If the total length of the string is an exact multiple of half-wavelengths of the wave, then the wave "fits" on the string.
- This means that the wave is resonant, with the string.
- Only specific wavelengths can fit on strings of fixed lengths, with nodes always at the ends, and otherwise nodes and antinodes alternating on the lengths of strings.
- There are several frequencies with which a string can be vibrated to produce the patterns.
- These frequencies and their associated wave patterns are referred to as harmonics.
- If a string is fixed at both ends, the wavelength of the first harmonic is equal to twice the length of the string.
λ₀ = 2l
f₀ = v/λ₀ = v/2l
- The wavelength of the harmonics when both ends are fixed is 2l, 2l/2, 2l/3, 2l/4 and so on.
- The corresponding frequencies are f₀, 2f₀, 3f₀, 4f₀ and so on.
- Standing waves on strings and ropes are usually between fixed ends, but it is possible that one, or both boundaries could be "free".
- If the two ends are free, then there will be antinodes at each end, so that the frequency of the first harmonic will be the same as for fixed boundaries, which has nodes at the ends instead.
- Although it is unusual for standing waves on strings to have both ends free, some standing sound waves may have both ends free.
Standing Wave Patterns of Air in Pipes
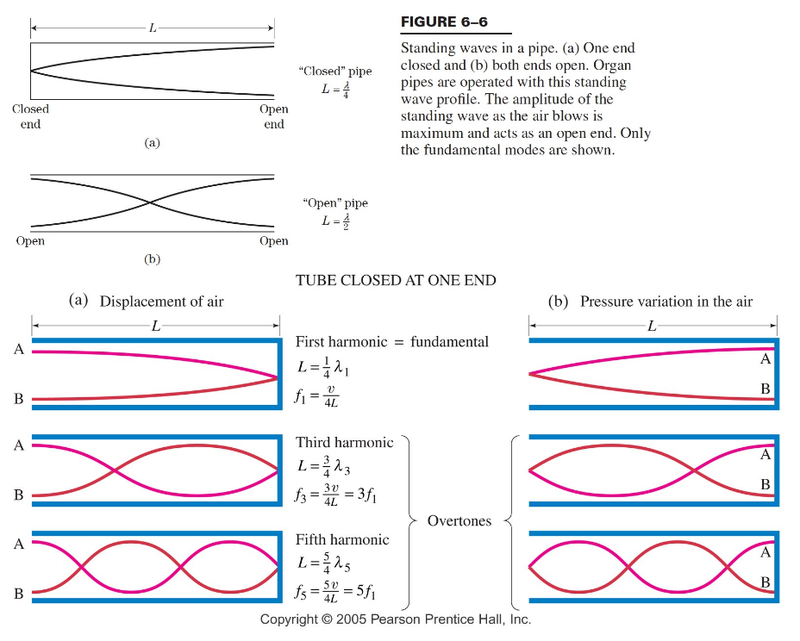
- Pipes can either have two open ends, one closed end, or two closed ends.
- Sound waves can be created in the pipes.
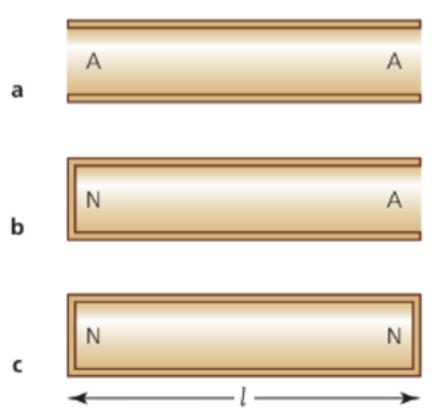
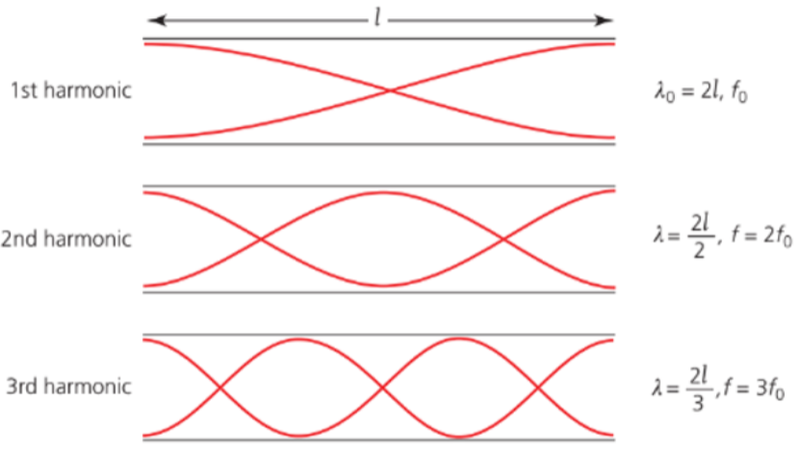
- For pipes with both ends open, the frequencies and wavelengths look like:
- It is the same for a pipe with two closed ends, except the ends are nodes instead of antinodes.
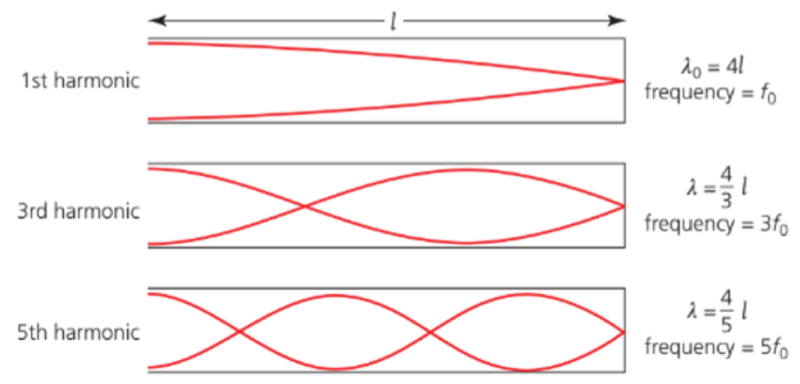
- For pipes that are open at one end and closed in the other, the longest wavelength is corresponds to a node at one end and an antinode at the other, meaning that the length should be 1/4th of the wavelength.
- Shortening the wavelength with each higher harmonic results in an addition of one node and one antinode.
- Thus wavelength is λ₀*1/(3+2n) for all harmonics after the first harmonic.
- Frequency increases by 2f₀ each time.
Sources
https://www.acs.psu.edu/drussell/Demos/StandingWaves/StandingWaves.html