What is Single Slit Diffraction?
- Single slit diffraction uses a single slit instead of two slits like in double slit diffraction.
- This results in a difference interference pattern, where there is a central maximum that is much wider and has higher intensity than other fringes.
- The other fringes, called the subsidiary maxima are equally spaced and get successively smaller in intensity and are half the width of the central maximum.
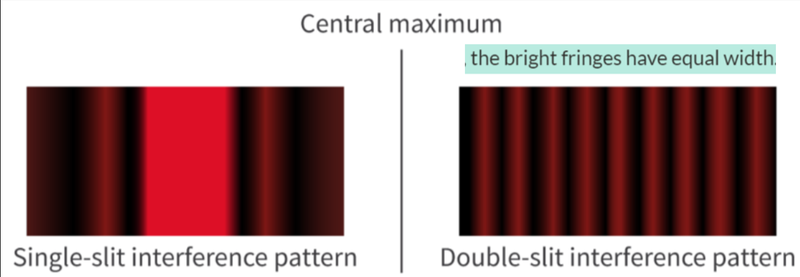
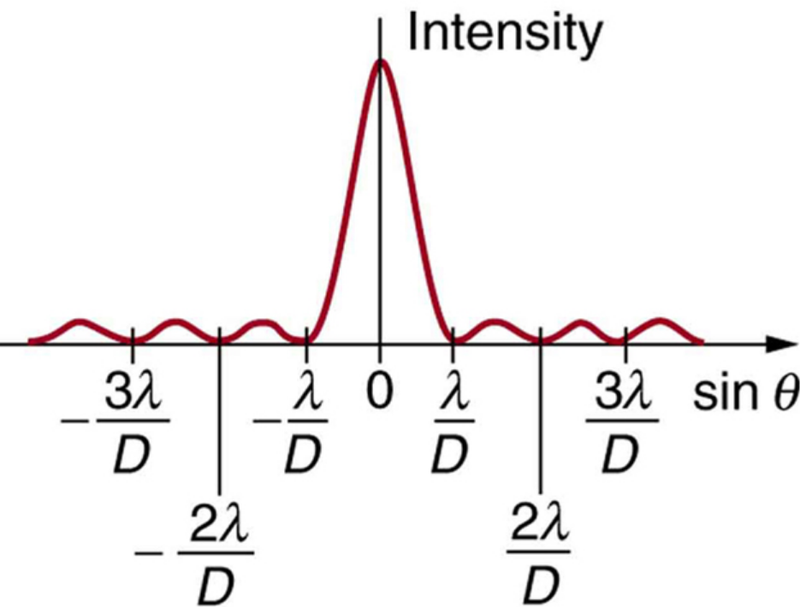
- The intensity pattern for single slit diffraction is similar to double slit diffraction except for the intense central maximum.
Single Slit Diffraction Equation
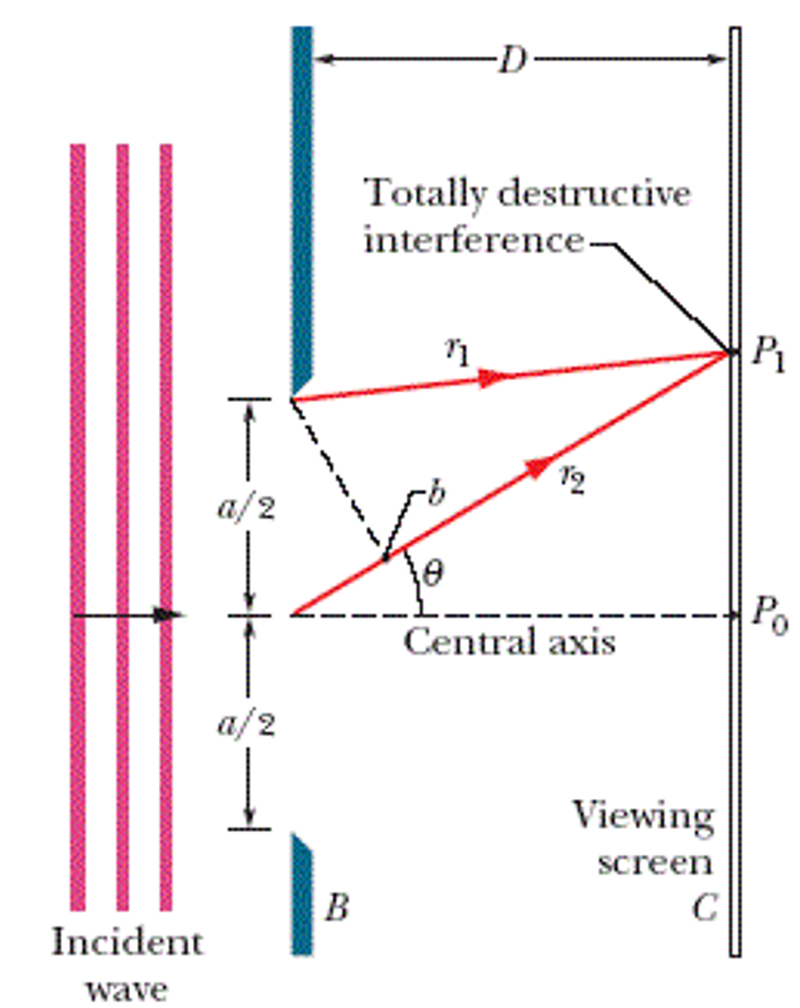
- In single slit diffraction, the angle from the normal to the slits of the first maximum is given as:
θ = λ/b
- Where θ is the angle to the normal from the center of the opening to the end of the central maximum.
- b is the width of the slit and λ is wavelength.
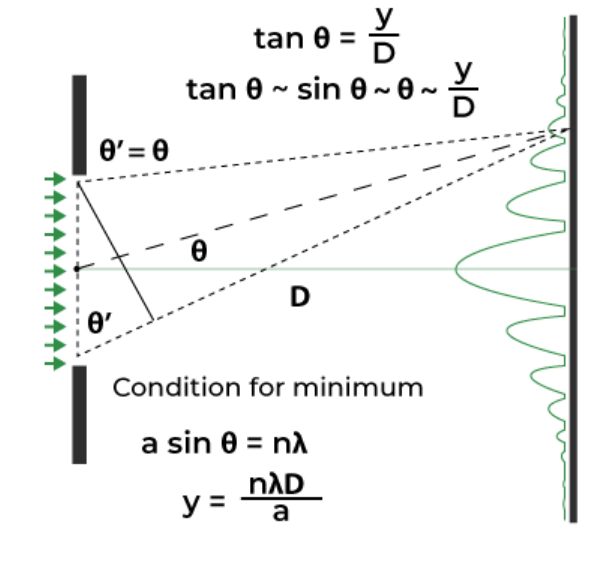
- Other diffraction minima will occur at angles, θ = 2λ/b, θ = 3λ/b, θ = 4λ/b and so on.
- Thus it can be described as:
θₙ = nλ/b
- Where n is an integer number.
- The angle θ can also be found through trigonometric equations, where a right triangle is formed where the distance between the slits and the screen is D and the distance between where the centre of the slit meets the screen and the central maximum is y.
- Thus:
tanθ = y/D
- Single slit diffraction generally occurs at very small scales, so that tanθ roughly equals sinθ which roughly equals θ.
- Thus:
θ = y/D
- Keep in mind that this equation is just an approximation, and might not give an accurate value, especially where more precise data is used.
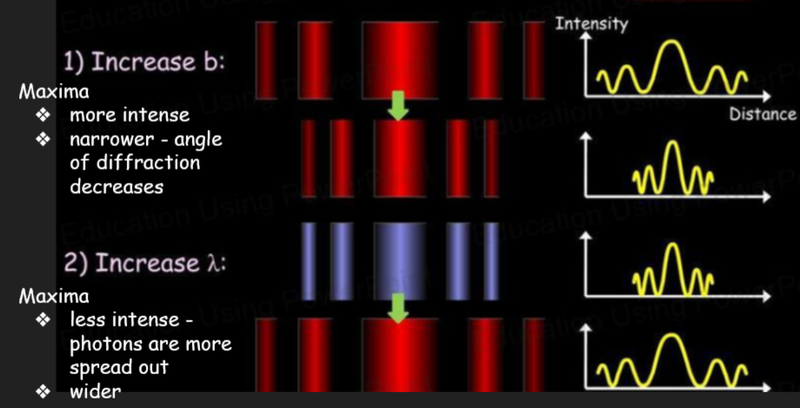
Changing Wavelength or Slit Size
- As θ = λ/b, changing the wavelength and slit size (on which b is dependent) have effects on how maxima and minima are distributed.
Sources