What is Simple Harmonic Motion?
- Simple harmonic motion is an oscillation in which acceleration is proportional to the displacement, but opposite direction.
- Acceleration is always directed back towards the equilibrium position due to a restoring force.
- A restoring force is always in the opposite direction to any displacement and aims to return an object back to the equilibrium point.
- As force is defined as F = ma, if mass is constant we can say that acceleration is proportional to the negative value of displacement.
a ∝ -x
- The minus sign shows that if the displacement is positive, the restoring force will be negative.
- And if the displacement is negative, the restoring force will be positive.
- Thus the the graph of acceleration to displacement should be negatively proportional.
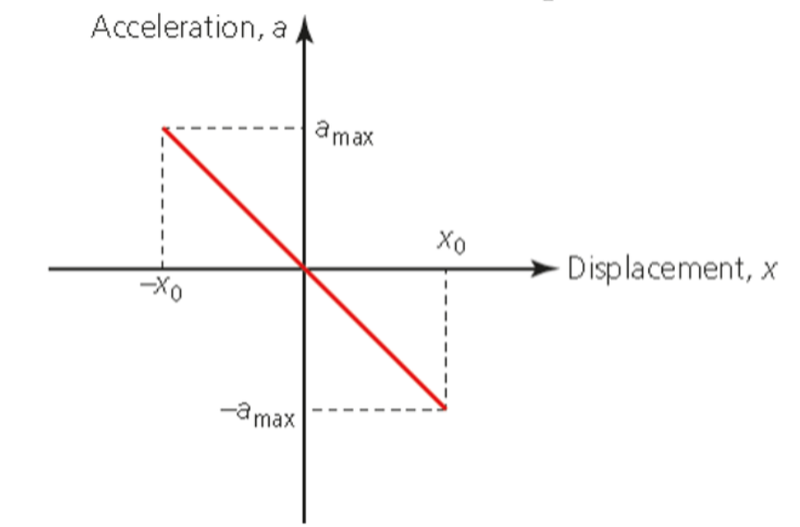
- When the displacement is zero, acceleration is also zero, and thus the body is said to be in equilibrium.
- However, even if there is no acceleration, the body still has velocity, causing its displacement to change once again, resulting in acceleration pulling it back.
- Oscillations are vibrations which repeat themselves, meaning that simple harmonic motion is repetitive.
- Simple harmonic motion is also isochronous, which means that the oscillations take equal times.
Examples of Simple Harmonic Motion
- For an oscillating mass which obeys Hooke's law, F = -kx, and as the spring constant k and mass (F = ma) are constant, the condition for simple harmonic motion is satisfied.
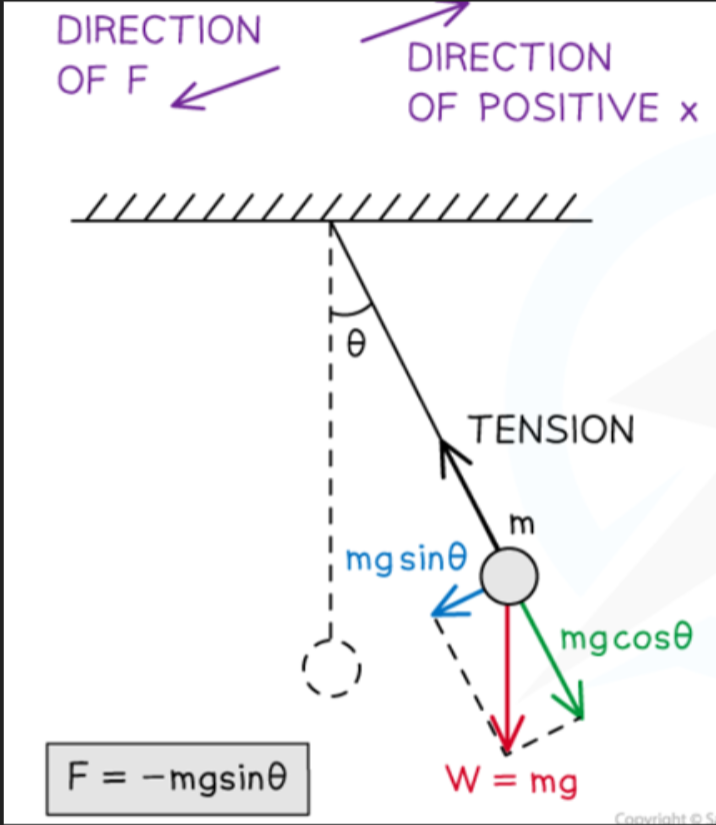
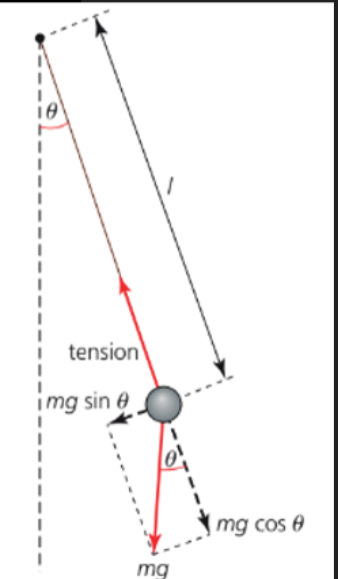
- However, simple harmonic motion can also occur in pendulums, as the restoring force mgsinθ is almost proportional to the displacement angle θ, as long as the angle is small.
Period and Frequency
- Period and frequency are used to describe oscillations of simple harmonic motion.
- They can show how long an oscillation takes or how long they occur and are closely related to each other.
Period
- Period, indicated by T, is the time in seconds a body takes to complete one complete oscillation (going back and forth).
- Period is the inverse of frequency:
T = 1/f
Frequency
- Frequency, measured in hertz (Hz) or cycles per second, is defined as the amount of oscillations that occur each second.
- Thus frequency is the inverse of period:
f = 1/T
Angular Frequency
- Angular frequency is similar to angular velocity from circular motion, and is calculated by:

- Angular frequency, like in circular motion, uses radians.
- One full oscillation is the same as one full revolution around a circle, 2π.
SHM Maximum Values
- The maximum values of displacement, velocity and acceleration during simple harmonic motion are given by:

- Where x is displacement, v is velocity and a is acceleration.
- ω represents angular velocity, which equals 2π/T or 2πf.
- Amplitude is the maximum distance from the equilibrium point a body goes during simple harmonic motion.
SHM Periods
Springs
- For a spring, there are two things that affect the period, the mass and the spring constant.
- The period is calculated as:
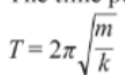
Where T is the period, m is the mass of the body, and k is the spring constant from Hooke's law.
Pendulums
- For a pendulum, the period is affected by the length of the string holding up the swinging mass, and the gravitational acceleration of free fall.
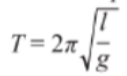
- Assuming the pendulum is on Earth, the gravitational constant of free fall should stay constant, meaning that the length of the string is the only variable that affects period.
Graphs of Simple Harmonic Motion
- The graphs of displacement, velocity and acceleration are all sinusoidal in shape, meaning they look like waves.
- All three have differing maximum and minimum points.
- Remember, velocity is the derivative of displacement and acceleration is the derivative of velocity.
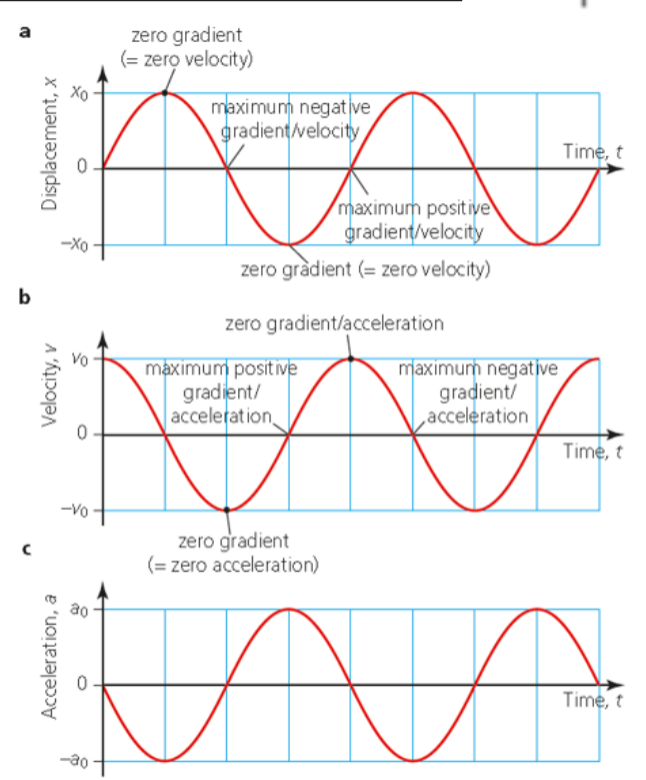
- The gradient of a displacement-time graph is equal to the velocity, and the gradient of a velocity-time graph is equal to the acceleration.
- This is what leads to the different maximum and minimum points.