Rotation of a Rigid Body

Properties of a Rotating Rigid Body

• The rotation of a rigid body can be described in terms of angular displacement, angular velocity and angular acceleration.
• You might recall that these properties are similar to the ones seen in circular motion.
• They describe similar properties, and likewise they use radians.

Angular Displacement

• Angular displacement is the change in angle through which a rigid body has rotated relative to a fixed point.
• The unit for angular displacement is radians.
• Angular displacement is defined as:

s = rθ

• Where θ is the angular displacement, or change of angle in radians.
• S is the length of the arc, or the linear distance travelled along a circular path, in meters.
• And r is the radius of a circular path, or distance from the axis of rotation, in meters.

• Recall that the formula for radians is:

θ = s/r

Angular Velocity

• Angular velocity is the rate of change of angular displacement, and thus is the derivative of it.
• It is calculated the same way as in circular motion:

• Similarly, if only velocity and radius are known, angular velocity can be found by rearranging the equation into:

ω = v/r

Angular Acceleration

• Angular acceleration is the rate of change of angular velocity, and thus is the derivative of angular velocity, and the second derivative of angular displacement.
• It is calculated the same way as in circular motion:

Graphs of Rotational Motion

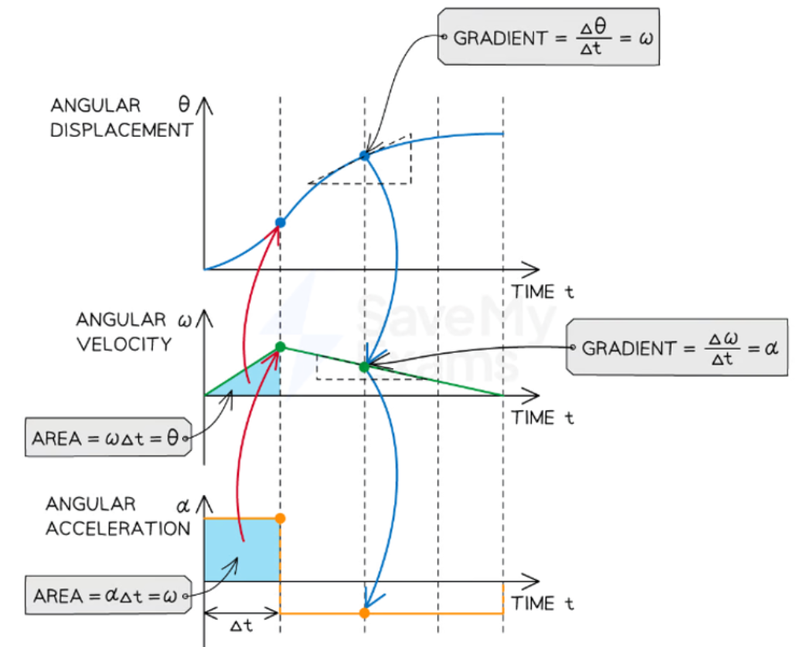
• As angular velocity and angular acceleration are the first and second derivatives of angular displacement respectively, we can determine several features from their graphs.

• The gradient of an angular displacement-time graph is the angular velocity.
• The gradient of an angular velocity-time graph is the angular acceleration.
• The area under an angular velocity-time graph is the angular displacement.
• The area under an angular acceleration-time graph is the angular velocity.

Equations of Motion

• The equations for rotational motion are actually very close to those of linear motion.
• The key difference is that linear displacement is substituted with angular displacement.
• This means that SUVAT also applies to rotational motion with constant angular acceleration!
• The biggest difference is that θωᵢωfαt doesn't have the same ring to it...