Free Fall
- In the absence of air resistance, all objects fall towards the Earth with the same acceleration, which is 9.8ms⁻².
- This is a constant, described as the gravitational acceleration of free fall, and denoted as g.
g = 9.8ms⁻²
- Sometimes you might see g described as its more precise value, g = 9.81ms⁻².
- Note that the value of g changes slightly on different parts of the Earth, and varies greatly when far from the Earth's surface!
- If gravity is the only force acting, all objects close to the Earth's surface will have the same acceleration, g.
- This is independent of their mass and whether they are moving down, up or sideways.
- However, not that this doesn't mean their velocity will be the same, only their acceleration.
Use of Gravitational Acceleration of Free Fall in SUVAT
- Don't forget that the unit for g is the same as that for acceleration, ms⁻².
- This means it can be substituted for acceleration, a, in SUVAT equations.
- However, keep in mind that this is only possible if there is negligible air resistance.
- If air resistance is considered, then acceleration would decrease and the SUVAT equations wouldn't be applicable.
- For an object falling from rest, distance is equal to height and initial velocity is equal to zero.
- Therefore we can rearrange the SUVAT equations into the following:
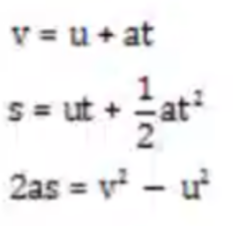
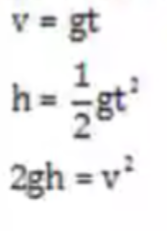
- Where:
g = gravitational acceleration of free fall
h = height
v = final velocity
t = time
u = initial velocity = 0
- It's usually not worth memorizing these equations, as they can be easily derived from the standard SUVAT equations.
Motion During Vertical Projection
- The motion of objects which are thrown and have uniform acceleration due to gravity are described by projectile motion.
- For vertical projection, an object is thrown directly upwards and it falls back to the ground.
- The path of a ball thrown directly upwards can be described in three phases.
Upwards Motion
- The ball starts with initial velocity u, but experiences a downward acceleration of 9.8ms⁻² due to gravity.
- As the initial velocity and gravitational acceleration are in different directions, the ball begins to slow down.
Instant of Being Thrown
- Time is zero.
- Initial velocity is maximum.
- Height is zero.
As the Ball Moves Upwards
- Height is increasing.
- Velocity is upwards but decreasing.
- Acceleration is downwards and constant.
Maximum Height
- Eventually the ball reaches a point where its velocity is equal to 0.
- At this point the ball changes direction, and starts going downwards.
- Height is at its highest point.
- Velocity is zero.
- Acceleration is downwards and constant.
- Time is halfway.
Downward Motion
- Now the ball is falling back down and it speeds up as it descends.
- Eventually it hits the ground with the final velocity being the same magnitude as the initial velocity, only in the opposite direction.
When the Ball is Falling Down
- Height is decreasing.
- Velocity is increasing downwards
- Acceleration is downwards and constant.
When the Ball Hits the Ground
- Height is zero.
- Time is maximum.
- Final velocity is equal to the negative of initial velocity (right before the ball hits the ground).
Sideways Projectile Motion
- We've discussed the motion of a ball being thrown straight up and falling back down.
- But what if the ball is thrown at an angle?
- The ball will move in an arc.
- However, it is most easily described by splitting the two components of motion, into sideways motion and upwards motion.
- This is done by splitting the vector of velocity into its horizontal and vertical components.
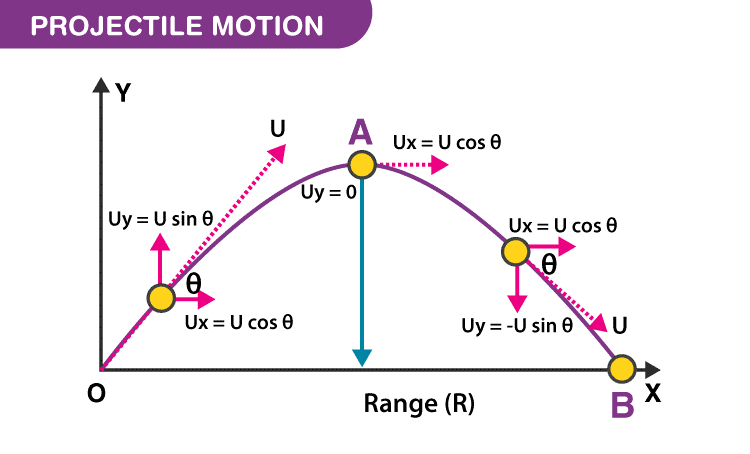
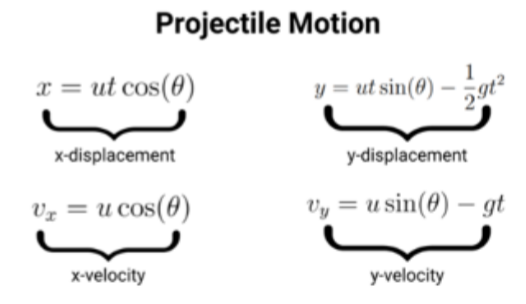
- With the absence of air resistance, the vertical motion of a ball thrown at an angle can be modelled just like the vertical motion of a ball thrown straight upwards.
- As the ball is going upwards and falling back down it is moving horizontally at a constant velocity (assuming no air resistance).
- Once the ball falls to the ground, it stops moving sideways (assuming it doesn't bounce).
- Therefore the horizontal distance it travels can be found by considering the time the ball takes to go up and fall back down.
Resistance Forces
- As an object moves through any viscous substance, such as air or water, there will be resistive forces acting on the object.
- This force is known as viscous drag force, notated as F.
- However, there is also an upthrust, notated as U, acting on an object moving down in a liquid, such as a ball falling in water.
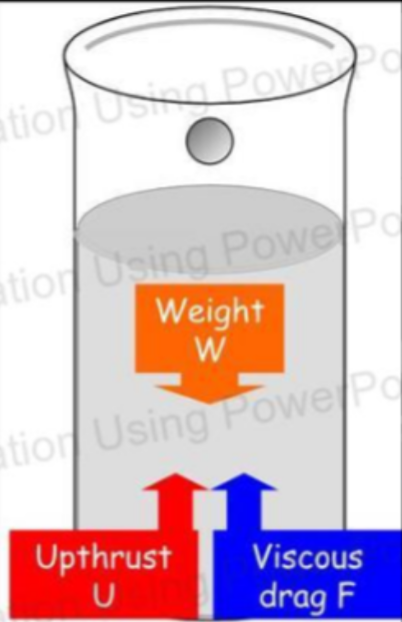
- The weight, which is the force on the ball as it is dragged down by gravity, stays constant.
- The upthrust, which is the weight of the fluid displaced, stays constant after the sphere is fully submerged.
- Viscous drag force is proportional to the velocity, so it increases as the ball gets faster.
- As acceleration depends on the force W pulling the ball down, if the forces U and F pushing the ball up are equal to W, then there would be no force acting on the ball, and acceleration would be zero.
- Therefore, velocity becomes constant at the point where W = U + F.
- Before this condition is met, the total forces acting on the ball are shown as Fₜ = W - (U + F).
- Therefore, when Fₜ = 0, then W = U + F.
- The velocity at which resistive forces equal the forces accelerating an object is called terminal velocity.
Terminal Velocity
- When an object reaches terminal velocity, its velocity becomes constant, and acceleration is zero.
- Terminal velocity occurs if air resistance is not neglected.
Effect of Fluid (Air) Resistance on Projectiles
- With air resistance considered, the velocity of the object will be reduced, due to the air particles colliding with the moving object and slowing it down.
- Air resistance reduces the range and height of a projectile, and its trajectory will no longer be parabolic.
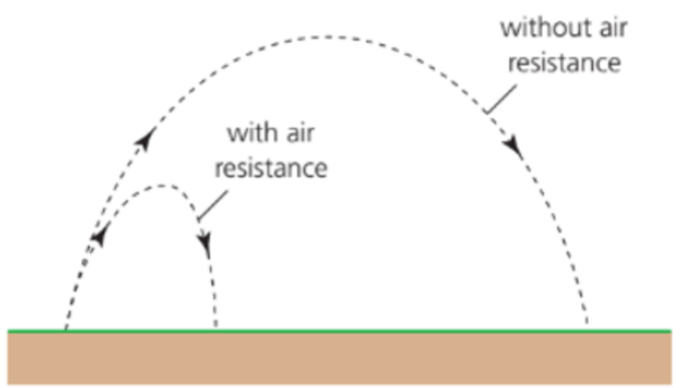
- Horizontally there is negative acceleration making the horizontal component of velocity decrease.
- Vertically, there is an increased magnitude of downward acceleration on the way up and a decreased magnitude of acceleration on the way down.
- This means the ball will ascend and fall down slower, reducing its maximum height.
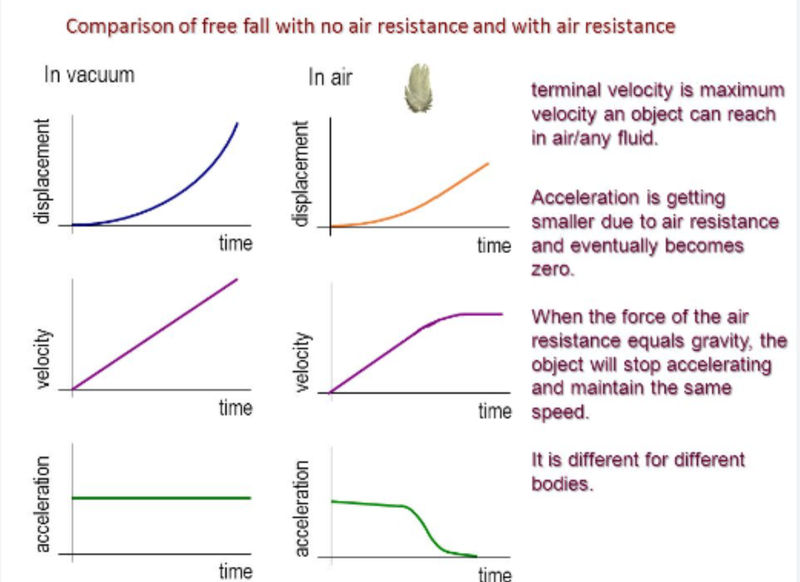
Graphs of Motion with Vertical Air Resistance
- The effect of air resistance on an object's motion can also be seen in its graphs.
Sources
https://edurev.in/studytube/Projectile-Motion/902dedcd-8bfa-4cbe-8171-f21a826feed1_t