Particle Motion in Gases
- Consider a container with a gas.
- If the volume is decreased:
- The particles should collide with the sides of the container more often, resulting in increased pressure.
- If the temperature is increased:
- The particles should collide with the sides of the container more often, resulting in increased pressure as well.
- This could lead to the container expanding.
Boyle's Law
- For a fixed mass of gas at a constant temperature (isothermal), the product of pressure and volume is constant.
- This is an empirical law, and is based on observation rather than a theoretical law based on combining or rearranging formulae.
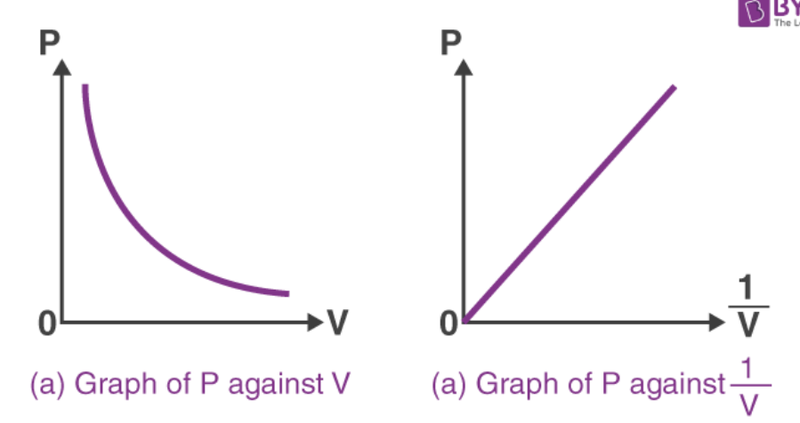
- As P*V = constant, the two values can be rearranged to show an inverse relationship.
- P = constant/V
- Boyle's law can also be used to find final volume or pressure where either value changes.

Gay-Lussac's Law
- For a fixed mass of gas at constant volume, the pressure is directly proportional to the absolute temperature.
- This is also called the "Pressure Law".
- Like Boyle's law, this is also an empirical law.
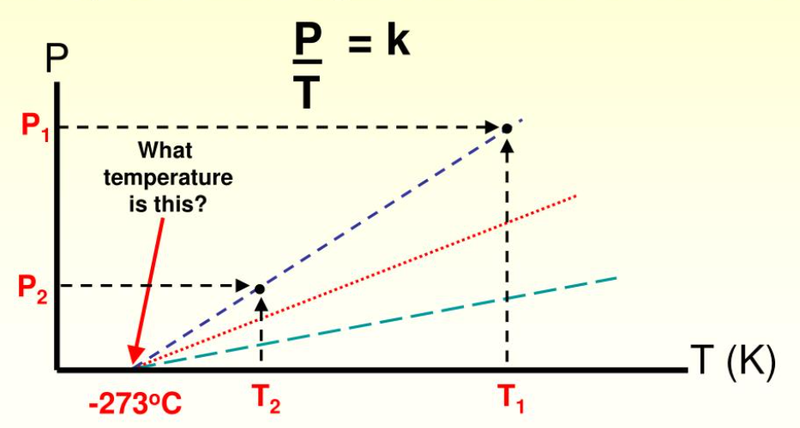
- At absolute-zero, there is zero pressure.
- This is because particles never collide with the walls of a container as they do not move.
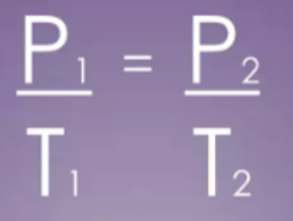
- This law shows that pressure and temperature are directly proportional.
Charles' Law
- For a constant mass of gas at fixed pressure, the volume occupied by the gas is proportional to its absolute temperature.
- Like the last two laws, this is also an empirical law.
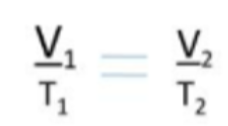
- This shows that volume and temperature are directly proprotional.
Combined Gas Laws
- You might have noticed that Boyle's law, Gay-Lussac's law and Charles' law are all very similar concepts.
- In fact, they can all be combined into a single equation.
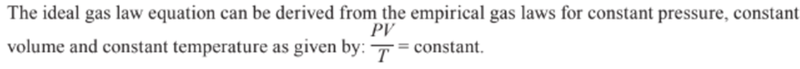
- This equation is very useful when it comes to finding changes in gas pressure, temperature or volume.
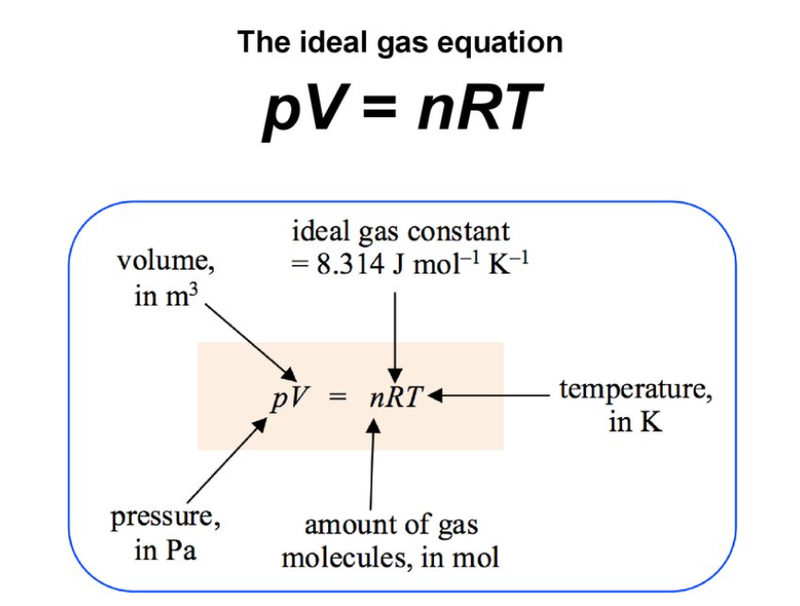
The Ideal Gas Equation
- The combined gas law can be further rearranged.
- For n moles of gas the constant from the combined gas law equation is R
- Boltzmann's constant is given as:
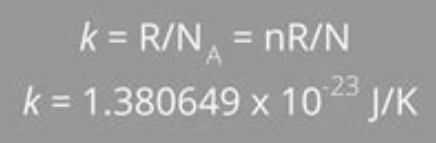
- Therefore the ideal gas equation can be rearranged as:
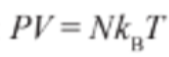
Pressure-Volume Diagrams
- The state of a known amount of gas, defined by values of its pressure, volume and temperature, can be identified as a point on a pressure-volume (PV) diagram.
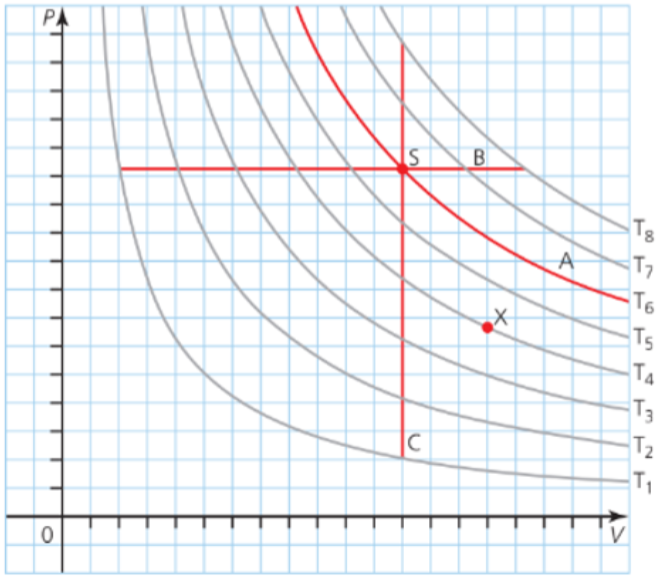
- Different temperatures lead to different curves.
- At a constant temperature, the gas will stay somewhere on the curve.
Ideal Gases
- Ideal gases are described in terms of the kinetic theory and constitute a modelled system used to approximate the behavior of real gases.
- The ideal gas equation and combined gas law are only applicable to ideal gasses, which:
- Have negligible molecular volume compared to the volume of their container
- Experience elastic collisions between particles and walls of the container
- Particles don't lose any kinetic energy when they collide with each other and the walls of the container.
- Have no intermolecular forces
- Their potential energy does not change
- Made of molecules which are identical perfect spheres.
- Real gases can behave differently from ideal gases if they have:
- Very low temperature
- Very high pressure
- Very high density
Kinetic Model of an Ideal Gas
- Just as temperature was a measure of the random kinetic energy of molecules for solids and liquids, it is also used to measure the random kinetic energy of ideal gases.
- If the temperature of a gas increases, so does the average speed, and thus kinetic energy of the molecules.
- The change in momentum of particles due to collisions with a surface gives the pressure in gases.
- From that analysis, we can determine that pressure is related to the average translational speed of molecules.
- This allows us to create the following formula:

Internal Energy in Ideal Gases
- The equation for internal energy is given by:

- Using ideal gas assumptions, the only energy an ideal gas has must be the kinetic energy of its molecules.
- And as internal energy is the sum of potential and kinetic energy, the internal energy of an ideal gas would be purely kinetic energy.
- Thus the internal energy formula can be rearranged into:
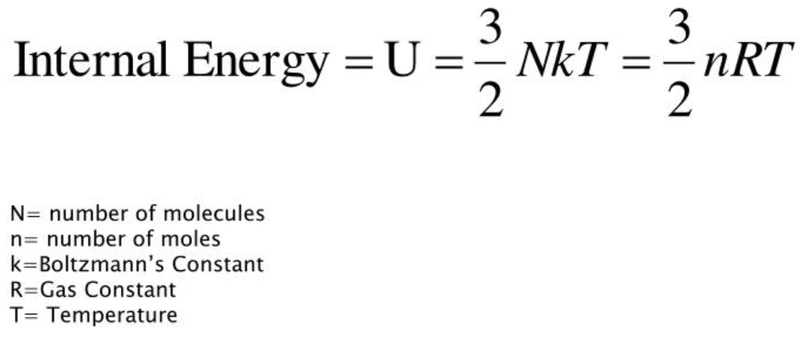
- An energy supplied to the ideal gas would cause an increase in its temperature, which is the kinetic energy of molecules.
- Therefore:

- Where Q = energy supplied.
Sources