Motion Force on a Charge in a Magnetic Field
- A stationary charge in a magnetic field will not experience any magnetic force.
- Only moving charges experience any magnetic force.
- Recall how magnetic force acts on a current (moving electrons)!
- A charge moving in a magnetic field will experience a magnetic force unless its motion is parallel to the magnetic field.
- The magnitude of the forces increases with the speed of the particle.
- The force is perpendicular to both the direction of its velocity and the magnetic field
- Fleming's Left-hand rule can be used once again to predict the direction of the magnetic force on moving charges in a magnetic field.
- We've used this for current, which was the movement of electrons.
- To adapt it to all particles, we simple replace the direction of the current with the velocity of the particle!
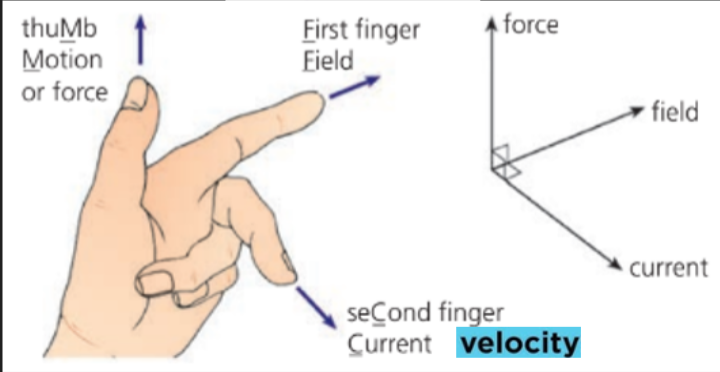
- Keep in mind that, for a negative charge, the current points in the opposite direction to its velocity!
- This is because the left-hand rule is based on conventional current, which moves from positive to negative.
- Hence movement from negative to positive (the movement of electrons) would be in the opposite direction to the conventional current).
Motion of Charged Particles in Uniform Magnetic Fields
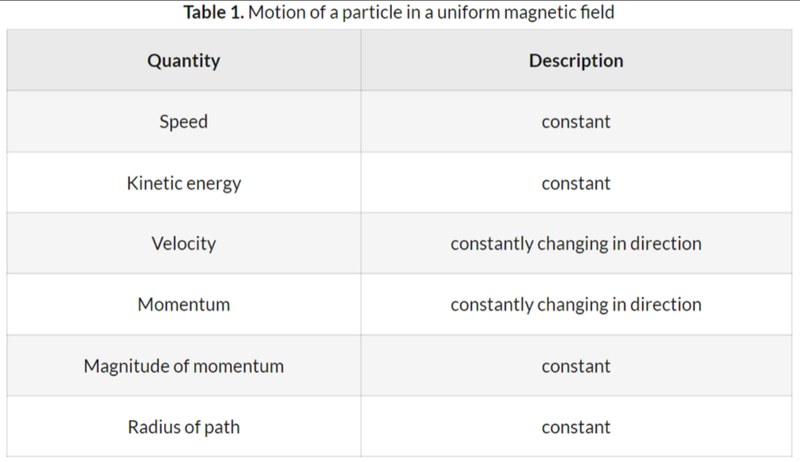
- A charged particle moving perpendicularly across a uniform magnetic field will follow a circular path.
- This is because the magnetic force is always perpendicular to its motion.
- Thus it functions as the centripetal force!
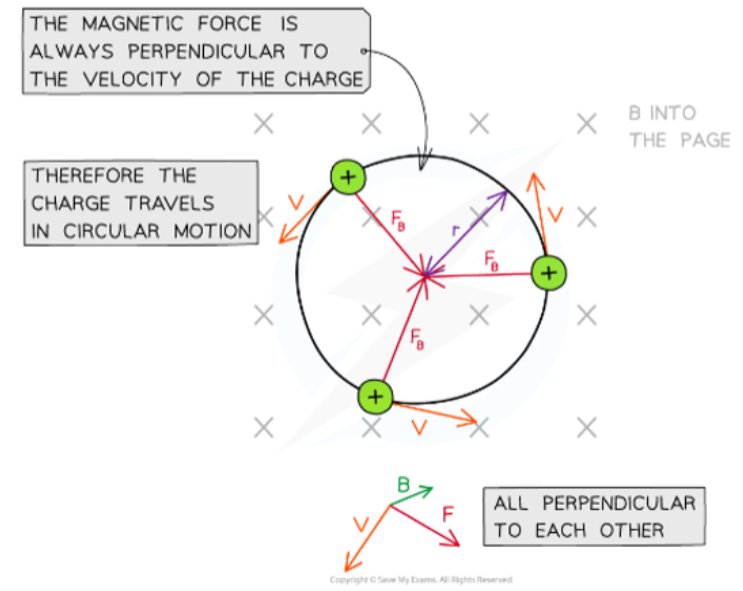
- During its circular motion in a perpendicular magnetic field, the speed and kinetic energy of the charged particle will remain constant.
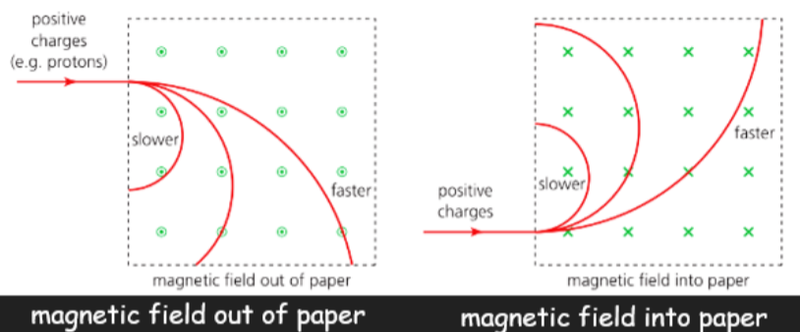
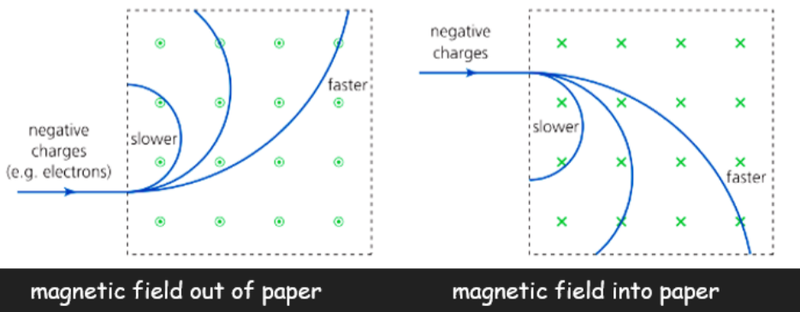
- Electron will move in the opposite direction by a proton as it is acted upon by an opposite force (remember the current is opposite to its velocity).
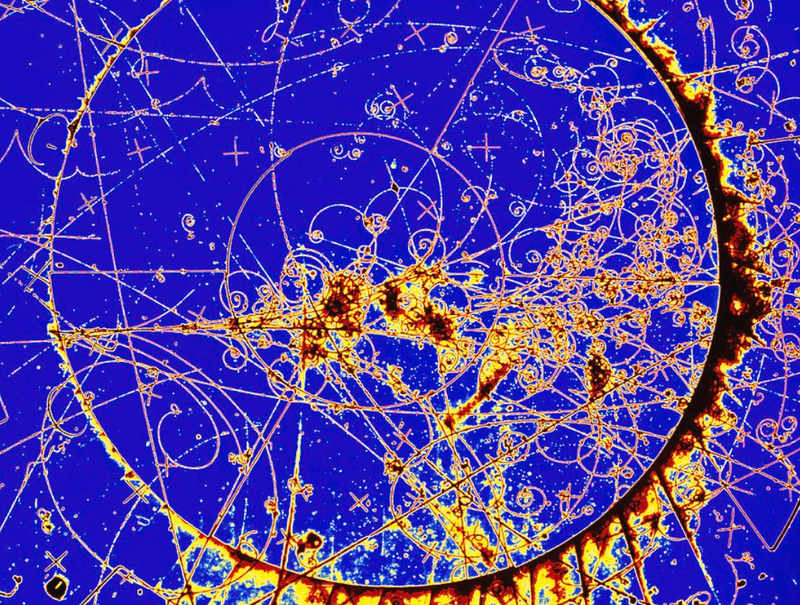
- This is what the motion of particles look like in a liquid hydrogen bubble chamber!
Recap
Magnitude of the Magnetic Force
- The magnitude of the magnetic force acting on a particle moving in a magnetic field is given by:
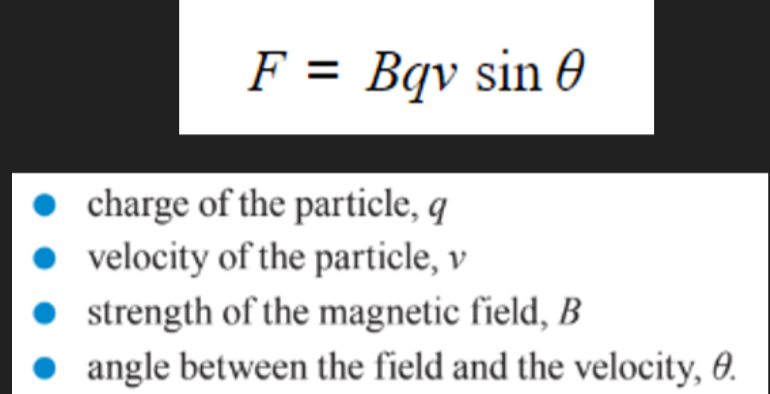
- B is the magnetic flux density, measured in teslas.
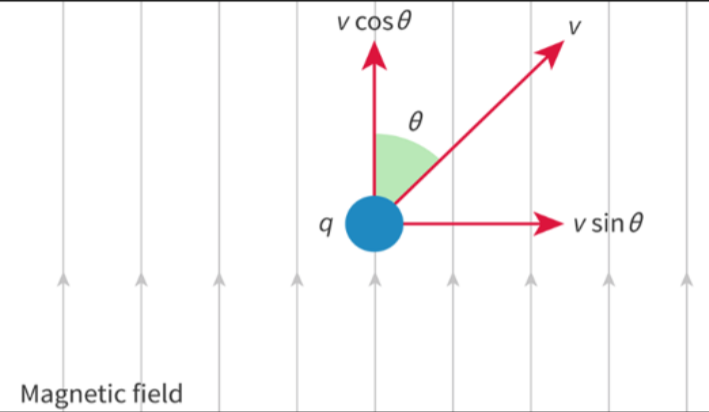
- If a particle is moving perpendicularly to a uniform magnetic field, then sin(90°) = 1.
- Centripetal force is given by:
F = (mv²)/r
- Where m and v are the mass and velocity of the particle and r is the radius of the motion.
- Therefore, for there to be circular motion, the magnitude of the magnetic force must be equivalent to the circular motion.

Charge to Mass Ratio of Particles
- From the formula for the centripetal force equating the magnetic force on a particle, we can find the ratio of mass to charge for particles.

Sources
https://fineartamerica.com/featured/streamer-chamber-photo-of-particle-tracks-cern.html