What is Gravitational Potential Energy?
- We've gone over gravitational potential energy before in kinematics.
- However, when it comes to planetary system, gravitational potential energy has a new meaning.
- It is the work done to assemble the system from infinite separation to the components of the system.
- As the force of a gravitational field is only zero if the two masses are an infinite distance apart, the zero of gravitational potential energy is chosen to be where the masses are separated by an infinite distance.
- The gravitational potential energy is the work that is done in moving those two bodies from infinite distance to a closer point.

- As work is only dependent on the component of the force that is parallel to the displacement, the path taken is not important.
- Gravitational potential energies are always given as negative values because positive work would be needed to separate the masses back to infinity, where a system once again has zero gravitational potential.
- This means the further two masses are, the less gravitational potential energy it has.
- Thus moving a two masses away from each other leads to work being done as the gravitational potential decreases.
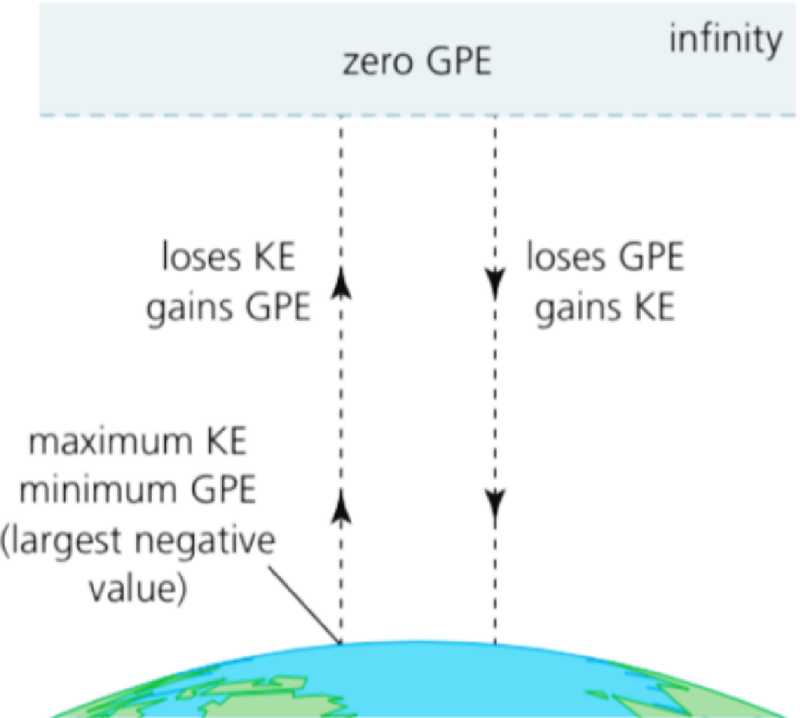
- As a mass moves towards the Earth, it gains kinetic energy, KE, but loses gravitational potential energy, GPE.
- This means GPE becomes more negative.
- As a mass moves away from the Earth, they lose kinetic energy, and gain gravitational potential energy.
- This means GPE becomes less negative.
- GPE is the highest right at the surface of the Earth, where the most work has to be done to separate the two masses.
- GPE can be thought of as a "debt" energy.
- It can be "paid off' by transforming other energies into gravitational potential energy.
Example
- Imagine separating two magnets, for example.
- Normally if you pull an object, you have to put in work to give it kinetic energy to get it to move.
- As for the magnets, you have to put in work to pull them apart so that they get to a state where they have no energy.
Gravitational Potential Energy Calculations
- We already know how gravitational potential energy is calculated when near the Earth's surface, which is:
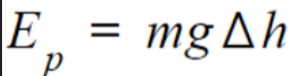
- However, for the gravitation potential between two masses we can use the formula:
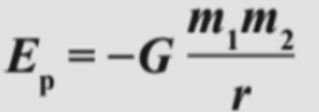
- The formula for the gravitational potential energy between masses close to the Earth is derived from this formula.
- Just as how work is force times displacement, gravitational potential energy is gravitational force multiplied by the distance between masses.
- This results in the denominator changing from r² to r.
- However, gravitational potential energy is also negative, unlike the normal formula for work.
Graphing Gravitational Potential Energy
- Gravitational potential energy is inversely proportional to the negative of radius, as the masses and gravitational constant stay constant.
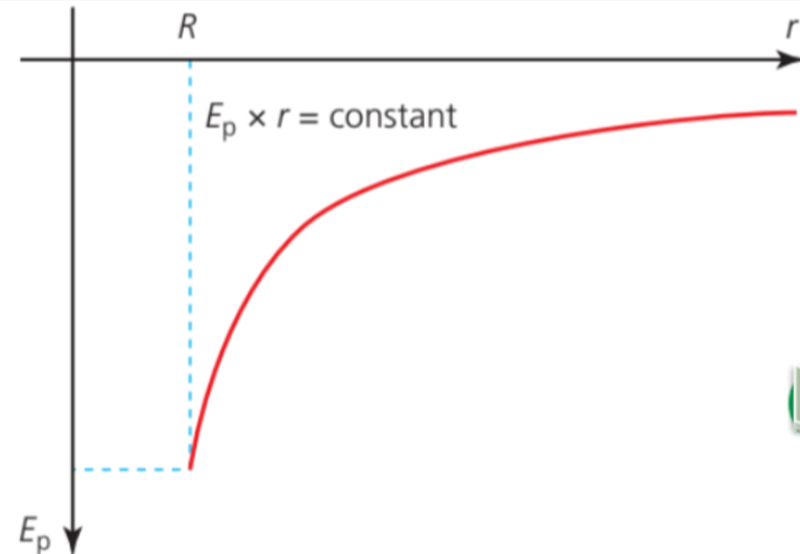
- The graph looks like a negative hyperbola, or f(x) = -1/x.