Gravitational Potential

What is Gravitational Potential?

Gravitational potential, not to be confused with gravitational potential energy, is the work done per unit mass in bringing a mass from infinity to a point.
It is the gravitational potential energy per unit mass.
Gravitational potential is indicated by V or Vg.

Gravitational potential is always a negative scalar quantity.
Gravitational potential is negative, because the negative symbol does not indicate direction, but instead shows that work needs to be done.

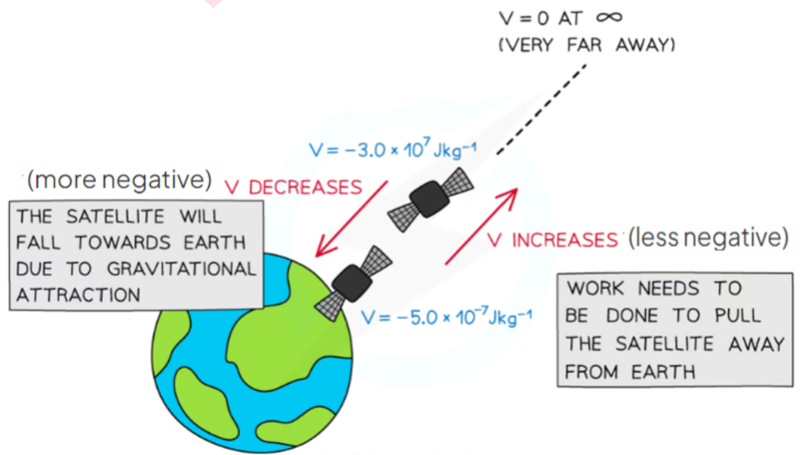
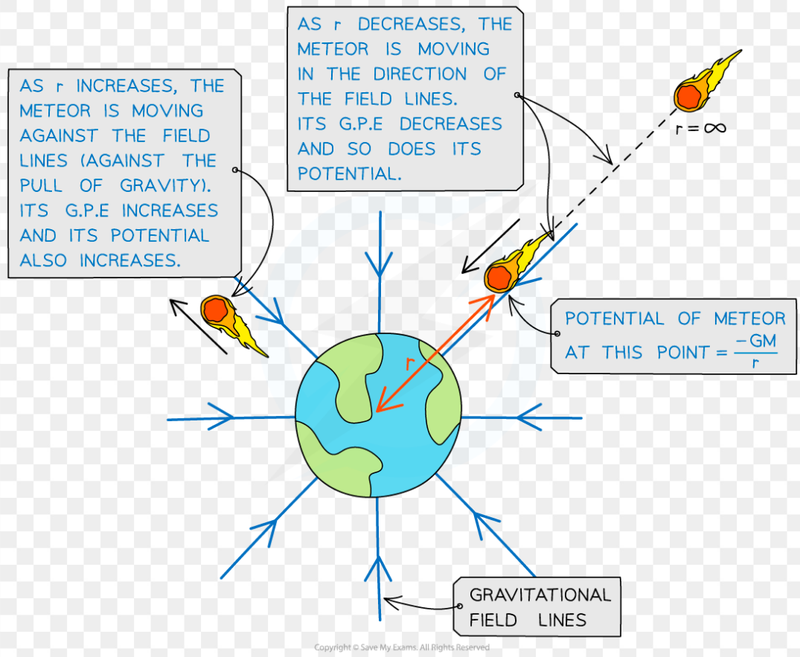
Gravitational potential associates each point in space with the work per unit mass that would be needed to move an object to that point from a fixed reference point in the gravitational field.

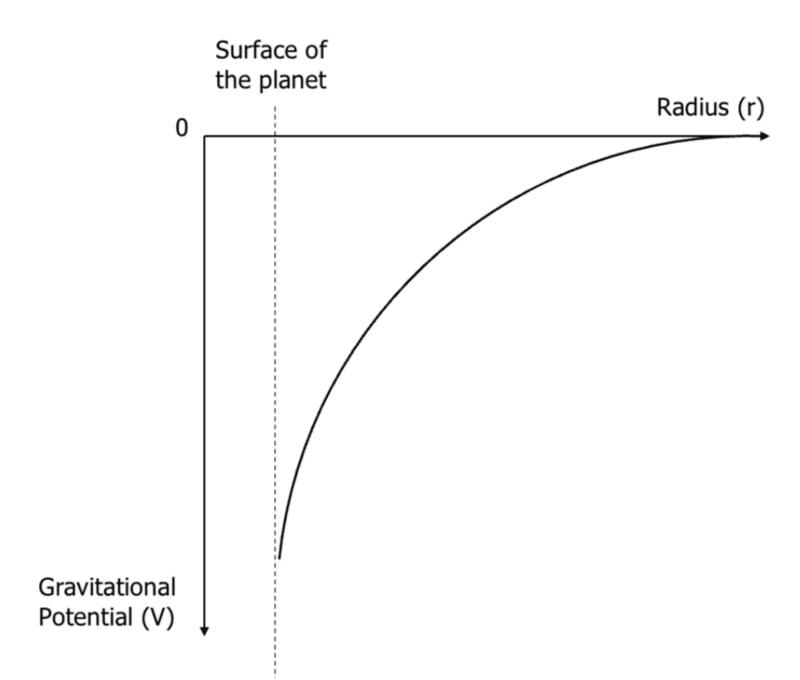
The graph for gravitational potential also looks like a negative hyperbola just like gravitational potential energy.

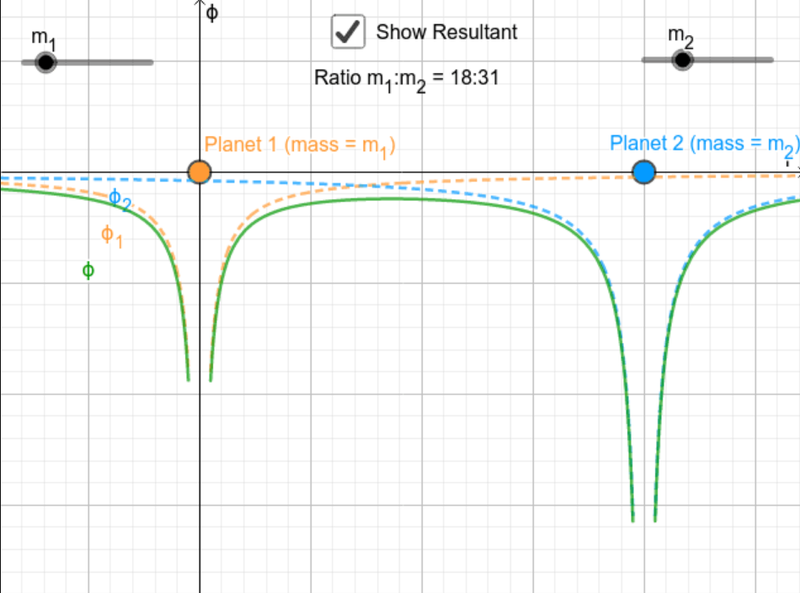
In the graph below, the red line represents the gravitational potential of the Earth and the black line the gravitational potential of the Moon.

The blue line is the combined gravitational potential.
The blue line is the sum of the two gravitational potentials, at every point which is why it is more negative than the red and black lines.

The potential energy decreases the closer you get to a mass, thus it decreases when you get either closer to the Earth or closer to the Moon.
The peak is the highest point on the line, where the gravitational potential of Earth is equal to the gravitational potential of the moon.

To make a journey from the Earth to the Moon, the peak must be crossed, which is the highest point on the blue line.

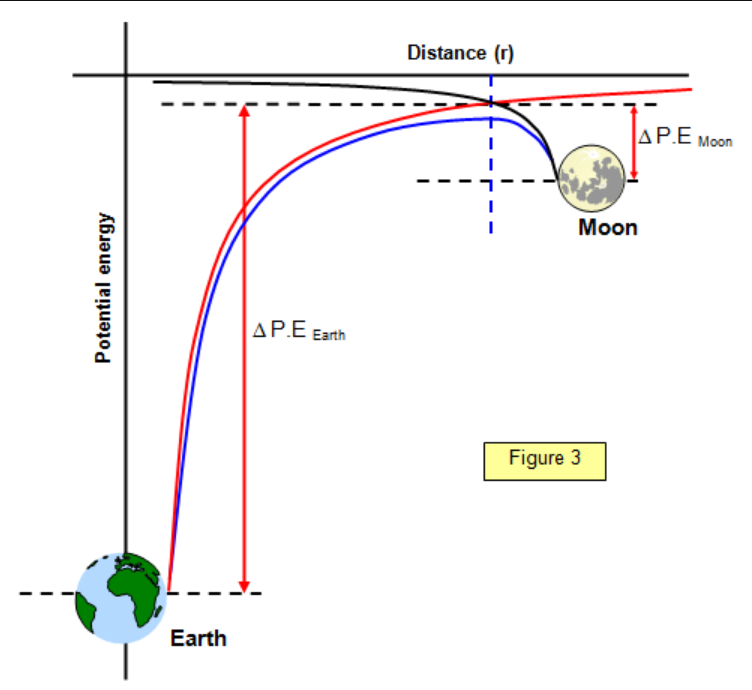
Gravitational potential starts much more negative at Earth, showing that it takes a lot more work to move to the peak from the earth, than it does to move to the peak from the Moon.
Likewise, gravitational potential ends up being far more negative if you start at the Moon and go to Earth, this shows that not much work has to be done, as it is instead "loaned" from the gravitational potential energy instead.
The gravitational potential is less negative if you start at the Earth and move to the Moon.
This means a lot more work has to be done.

Note that the position of the planets on the graph doesn't show their actual positions, it is only used to show that gravitational potential is lowest at the point on their radii.

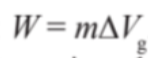
Recall how gravitational potential is the gravitational potential energy per unit mass.
Multiplying the change in gravitational potential by the mass will give us the change in gravitational potential energy, which is equal to work done.
The formula is derived through:

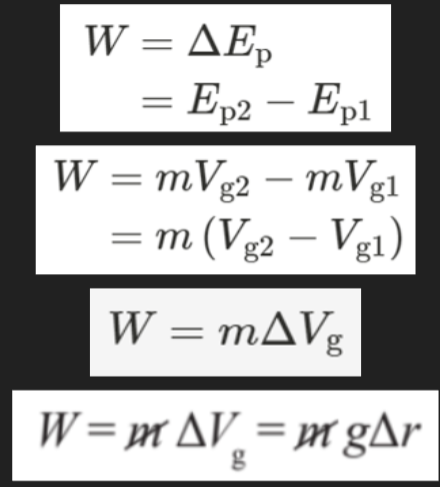
This formula also shows that the change in gravitational potential is equal to the gravitational field strength times the change in radius.

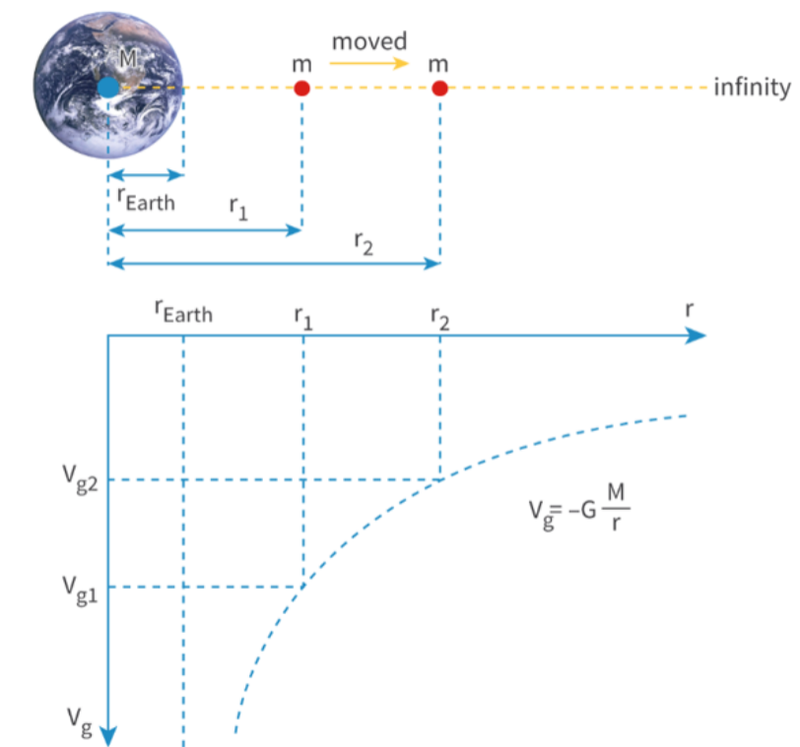
On a graph of gravitational potential to distance, the gradient is the change in gravitational potential over the change in distance, which is equal to:
GM/r²
This is therefore also the derivative of gravitational potential, which is equal to the gravitational field strength, g!

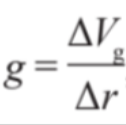
Oftentimes, Δr is a small enough distance that the value of g doesn't change significantly.
This is why we can treat g as a constant in projectile motion calculations.

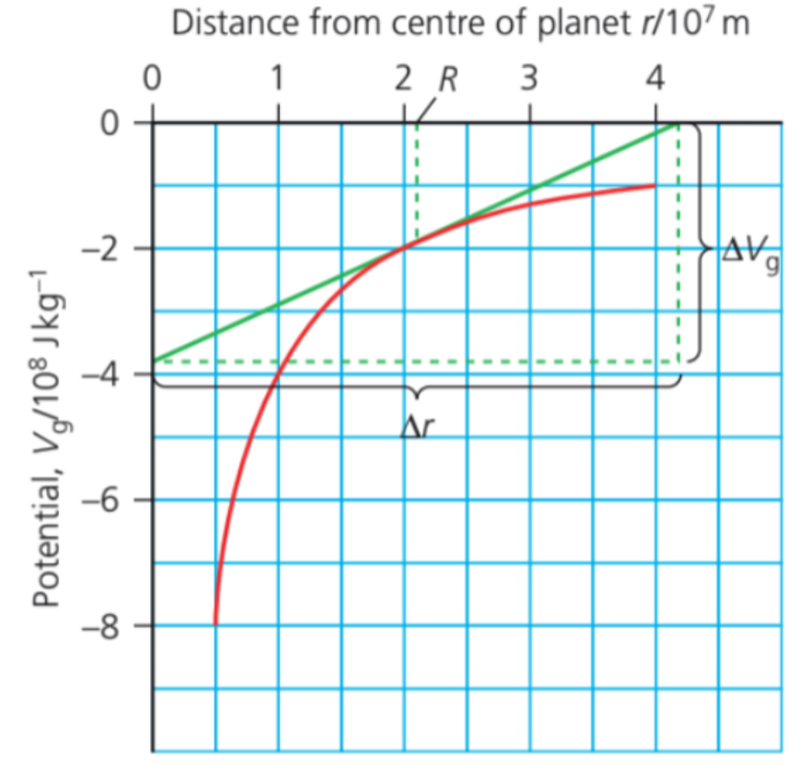
In the above graph, the green line is the tangent of the curved line, and its gradient represents the gravitational field strength g at that point.

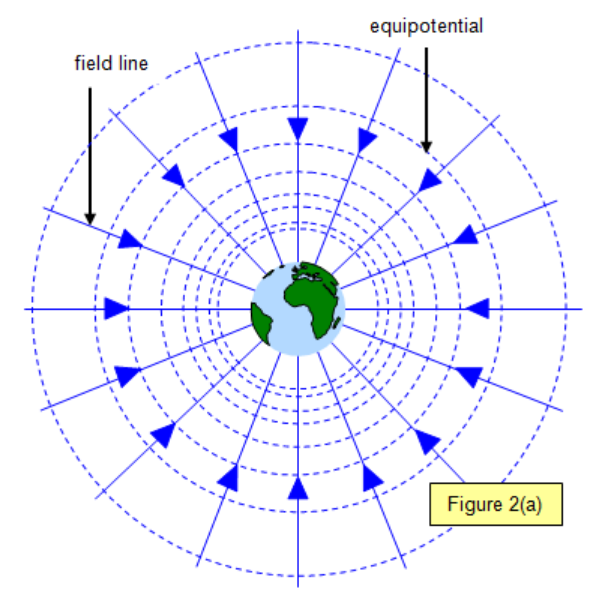
Gravitational equipotential lines show lines where it takes an equal amount of work to get from one line to the other.
The change in gravitational potential is equal between the lines.
The spacing between the lines increases the further they are as the gravitational field strength, which is the rate of change of gravitational potential, gets smaller.

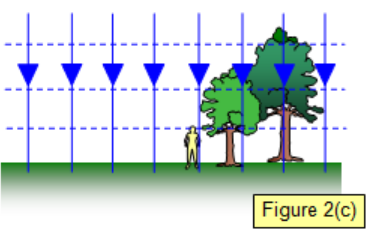
When close to the surface of the Earth, just like field lines, equipotential lines become flat and uniform.

As equipotential lines are always perpendicular to gravitational field lines, some weird things happen when there are two masses.

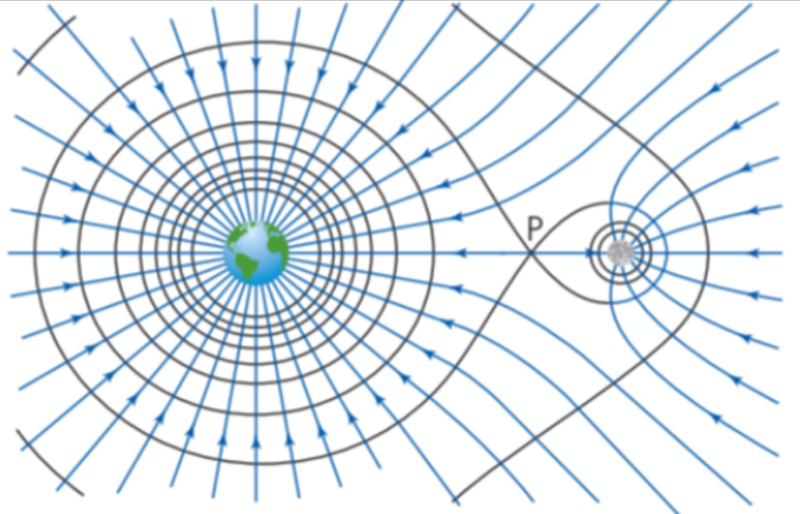
Notice how point P, is actually the peak from the gravitational potential to distance graph!

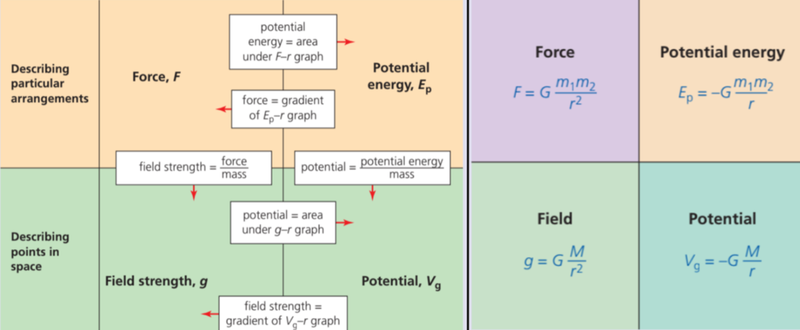
If you struggle to remember which values are the gradients of which graphs and which are the areas underneath those graphs, keep in mind how derivatives work.

Gravitational field strength is actually the derivative of gravitational force with respect to mass, and similarly gravitational potential is the derivative of gravitational potential energy with respect to mass.
However, you will likely never see any of these values graphed with respect to mass as it often stays constant.

Sources

https://www.hanlin.com/archives/711124