What is a Gravitational Field?
- Gravity is a field force, meaning it exerts itself over a distance.
- A gravitational field is the region of space in which a mass experiences a force due to the presence of one or more other masses.
- While a gravitational field covers an entire area, field lines can be drawn to help visualize its effect.
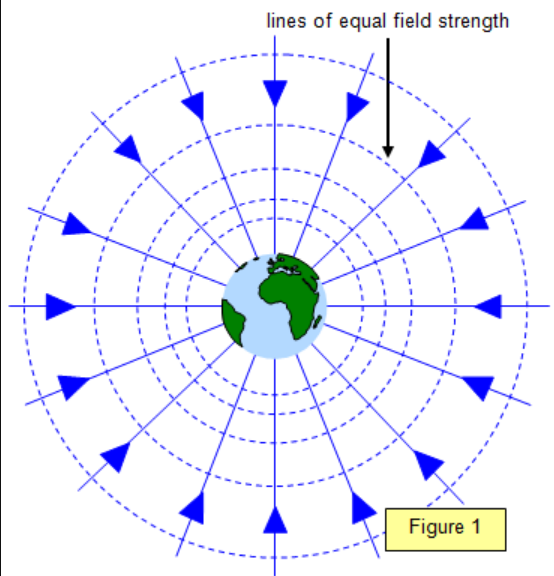
- The field lines are pointed inwards, showing the direction of the force, which is towards the attracting body.
- The field lines spread outwards and also get weaker with increasing distance.
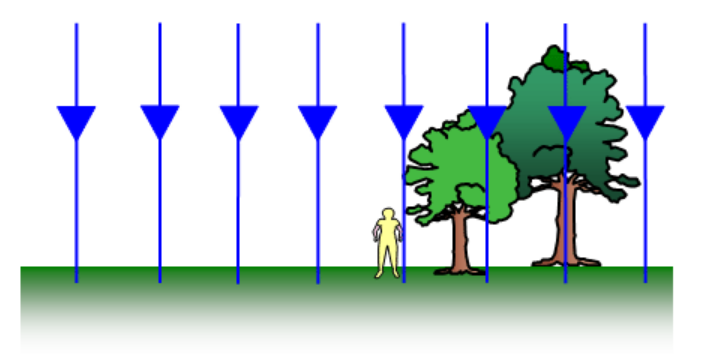
- While field lines appear spread out when far from the surface of the Earth, they appear uniform when close to the surface of the Earth.
- If two masses are close together, then their fields lines will warp.
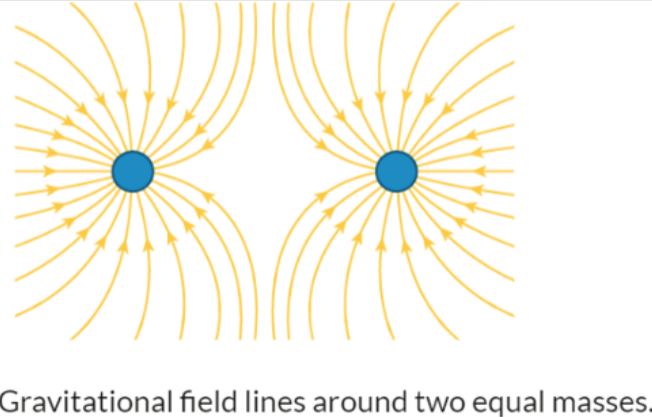
- This is because the field lines show the direction of the force experienced by a mass in the field.
- Imagine the above diagram shows the gravitational field of two planets, and a satellite is moved somewhere in the field and left to rest.
- If the satellite is at the left side, then it will be pulled towards the left planet.
- And likewise, if the satellite is placed on the right side, it will be pulled towards the right planet.
- However, if the satellite is placed in-between the two planets, in the area where there are no field lines, then it does not move at all.
- This is because both planets (assuming they are the same distance to the satellite and of the same mass) pull the satellite towards themselves with equal force, leading to the forces cancelling out.
Connection of the Acceleration of Free Fall
- We're used to using the letter g to indicate the acceleration of free fall due to gravity, or simply the acceleration due to gravity.
- However, this constant has another use.
- It also indicates the gravitational field strength, and is measured in newtons over kilograms.
- These are the same units as that for the acceleration due to gravity, just rearranged.

Gravitational Field Strength Around a Planet
- Consider an man on the Earth.
- His weight would be equal to W = mg, where W is his weight, m is his mass and g is the gravitational acceleration of free fall.
- However, we also know the gravitational force he experiences due to the Earth, which is (GMm)/r², where M is the mass of the Earth.
- The gravitational force he experiences must be equal to his weight.
- Therefore we can equate the two equations:

- The value g is a vector quantity.
Gravitational Field Strength at a Point Along a Line Joining Two Masses
- In general, if two or more masses are creating gravitational fields at a certain point, then the total field is determined by adding the individual fields, remembering that they are vector quantities.
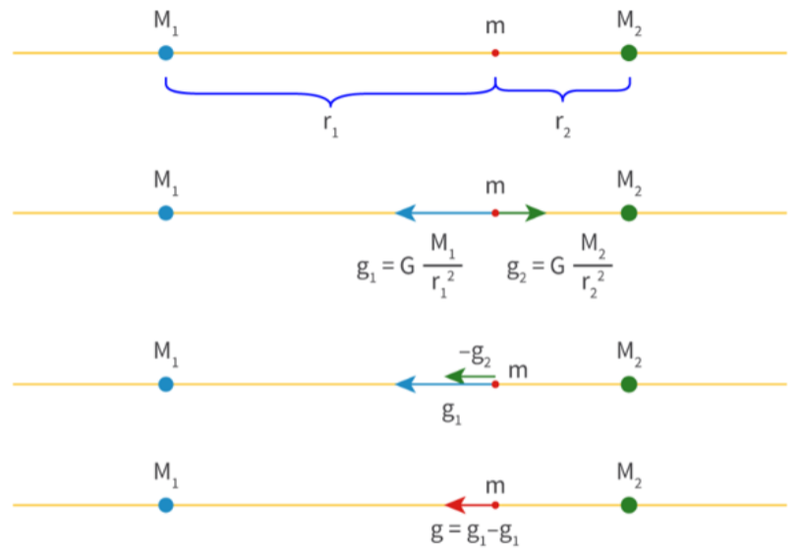
- It is possible to calculate the gravitational field strength at a point along a two-dimensional plane, but then things get a lot more complicated as you would need to decompose vectors first.
Gravitational Field Strength Graphs
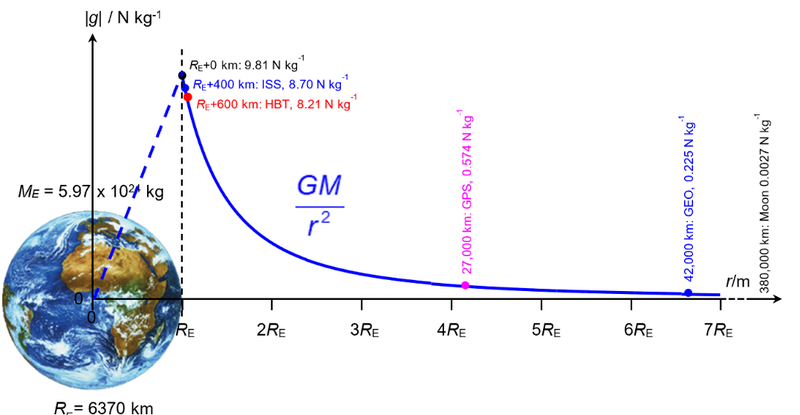
- We discussed how gravitational field strength decreases exponentially with increases in the distance, r.
- This can be seen on a graph, where the relationship between distance and gravitational field strength looks like a hyperbolic function (1/x).
- The gravitational field strength is based on the shell model, which states that there is no gravitational field strength inside of a mass.
- Thus it is highest exactly on the surface of the Earth, and then starts decreasing the further you get away.
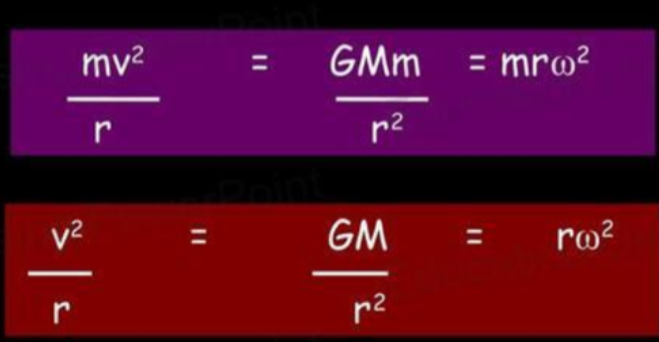
Gravity and Centripetal Force
- An orbiting object is moving in a pattern similar to circular motion, as its velocity is tangential to the path of its orbit, and it is constantly turning inwards.
- Thus must mean there is a centripetal acceleration, and thus a centripetal force pulling it inwards.
- If the satellite has a speed of v and a mass of m, we get:
Sources
https://spark.iop.org/collections/gravitational-fields
https://xmphysics.com/2023/01/02/7-2-2-gravitational-field-of-a-point-mass/