What are Waves?
- Waves are any type of repetitive, isochronous oscillation.
- When drawn out, the graph resembles a wave.
- Waves have several key properties that are useful to know when analyzing them.
Graph Properties
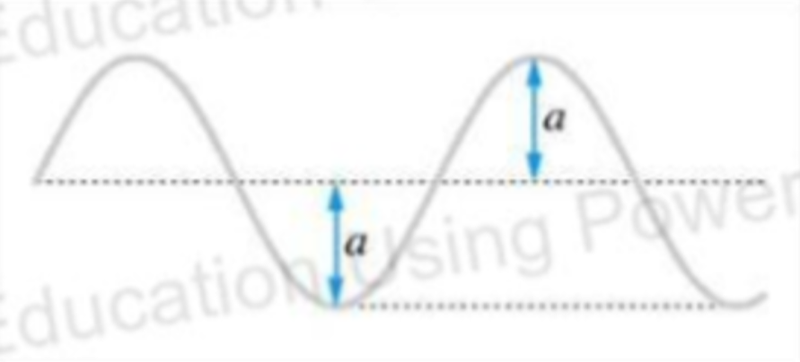
Amplitude
- Amplitude, A, is how far the wave gets away from the equilibrium point of zero.
- It is measured in meters.
- It is equal to half of the difference between the maximum and minimum points of a wave.
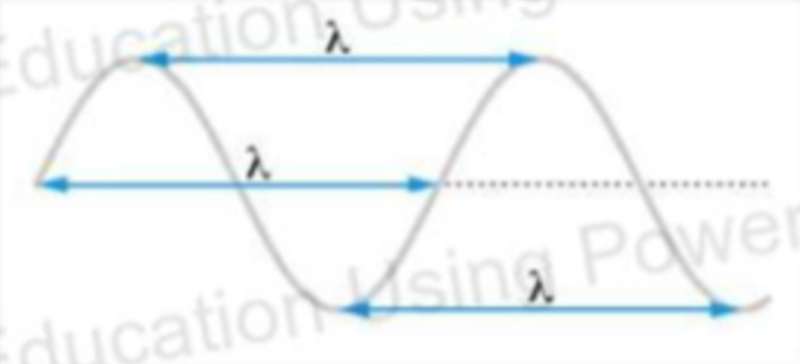
Wavelength
- Wavelength, λ, is the distance between two corresponding points on a wave and is measured in meters.
Period
- Period, T, is the time interval required by a wave to complete one cycle.
- It is measured in seconds.
- It is the difference between two corresponding points on a simple harmonic motion graph if the x-axis is time.
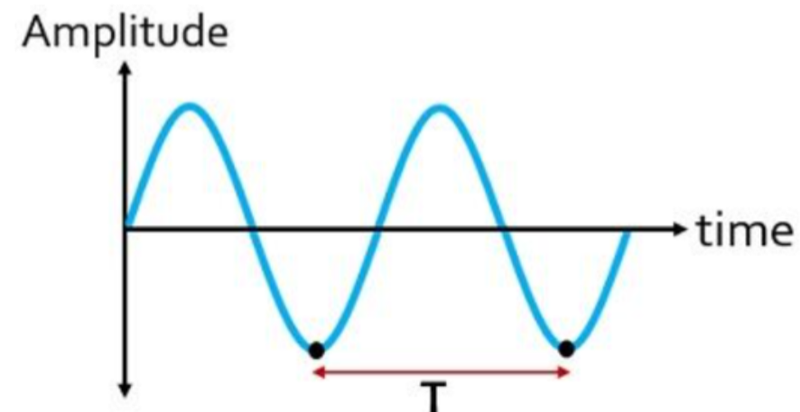
- Pay close attention to graphs as to not confuse period with wavelength!
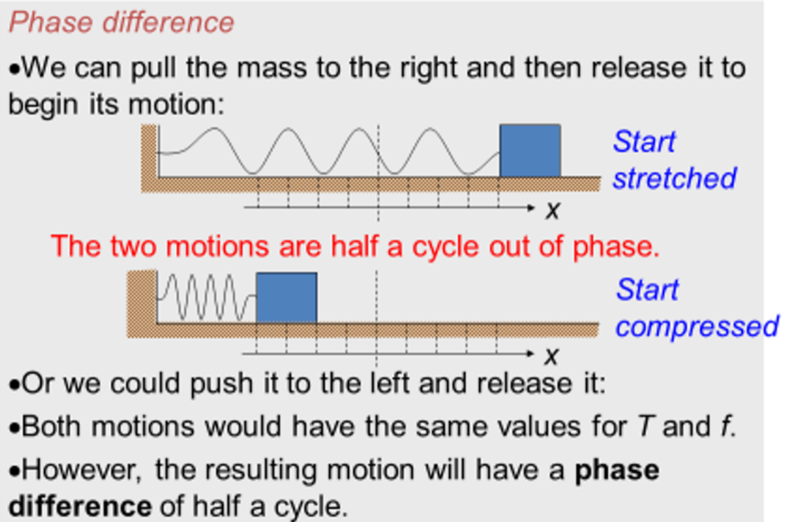
Phase Difference
- The phase difference is the difference between two waves that have the same frequency, but oscillate differently to one another.
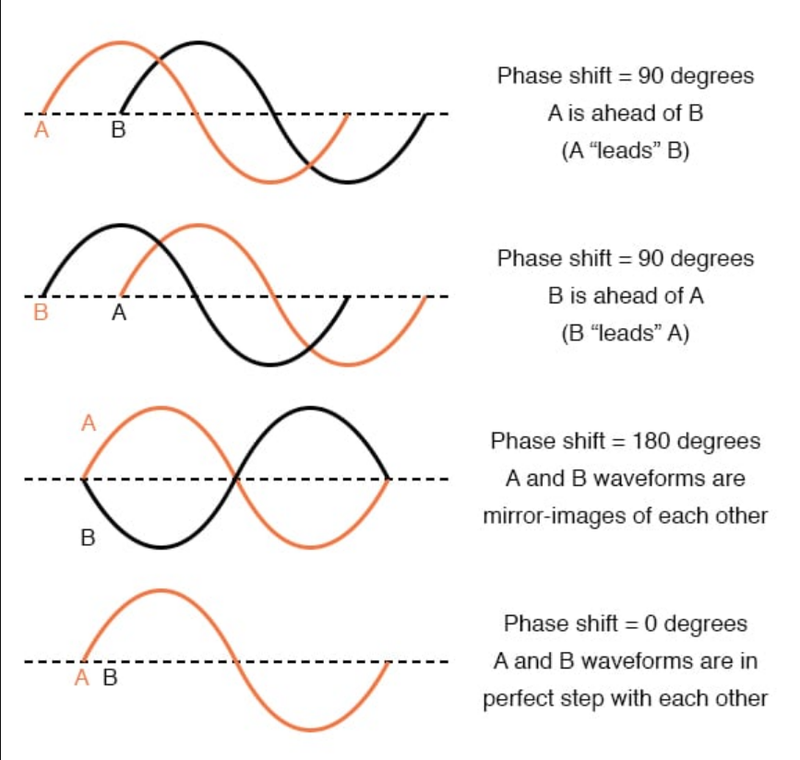
- Phase difference is generally measured in radians, and it is the difference between corresponding points on one wave and the other.
- Keep in mind that waves of different amplitude can still be in phase, as long as their oscillations occur at the same times.
Example
Phase Angle
- The phase angle of an oscillation, given by ϕ, is the fraction of an oscillation (expressed in terms of π) that occurs between when it has zero displacement, and a sine wave which has zero displacement at time t=0.
- It is effectively the phase difference between a specific wave and a standard sine wave.
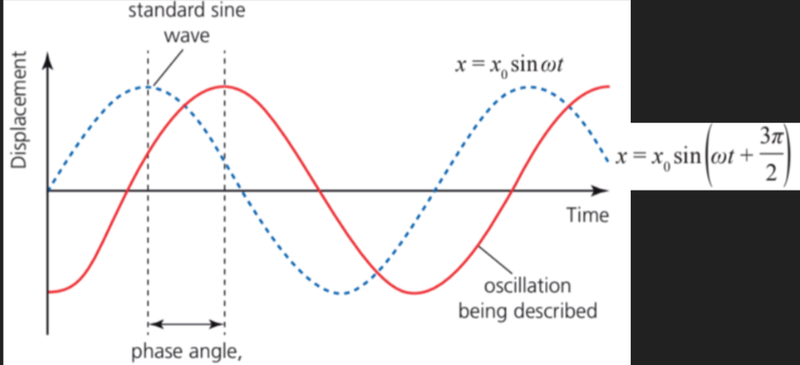
- While it can be easy to discern the phase angle if the wave is displaced by 2π or π/2, special equations are needed for more complex problems.
- Phase angle is zero if the displacement is zero when time is equal to zero, as that is how a normal sine-wave looks.
Equations for Simple Harmonic Motion
- A particle undergoing simple harmonic motion can be described using the phase angle.
- Problems can be solved using:
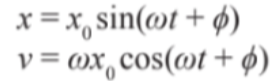
- Where x is vertical displacement, x₀ is amplitude, v is linear velocity, ω is angular frequency, t is time and ϕ is the phase angle.
- These equations can also be rearranged to find the phase angle.
Using Equations for SHM Graphs
- Previously we discussed how displacement, velocity and acceleration during simple harmonic motions appeared as similar sine wave graphs, yet shifted.
- By using the phase angle, we can also determine the velocity and acceleration that occurs during simple harmonic motion.
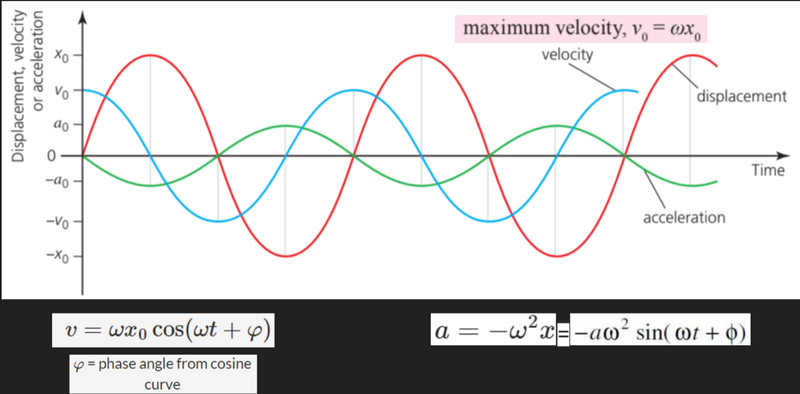
- As velocity is defined using cosine, we look at the phase angle between it and the standard cosine function.
- As acceleration is angular velocity squared multiplied by displacement, the displacement can be substituted with its equation using phase angle.
- The formula is negative as acceleration is in the opposite direction to displacement.
SHM Energy Changes
- All mechanical oscillations involve a continuous exchange of energy between kinetic energy and some form of potential energy.
- For example, in a mass-spring system, the maximum potential energy is Eₚ =1/2*kx² and the maximum kinetic energy is 1/2*mv².
- Likewise, in a pendulum, the maximum potential energy is Eₚ = mgΔh and the maximum kinetic energy is 1/2*mv²
- Energy will be continuously transferred between potential and kinetic energy.
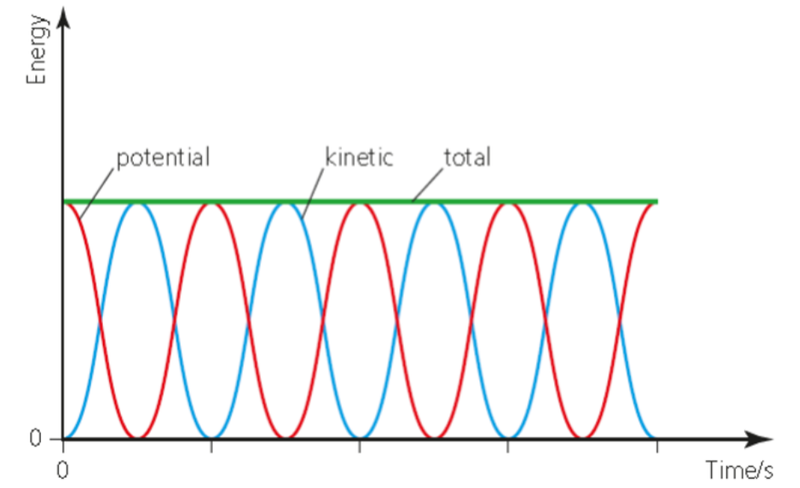
- The total energy of a simple harmonic motion system is proportional to the square of its amplitude.
E ∝ A²
Energy Calculations
- Problems relating to energy levels in simple harmonic motion can be solved using:
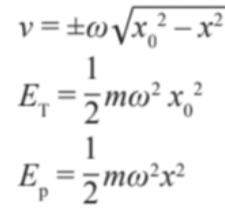
- Where v is velocity, ω is angular frequency, x₀ is amplitude and x is displacement.
- Eₚ is potential energy and Eₜ is total energy.
- In these calculations, energy is a function of displacement.
- Notice how in the calculation for velocity, the answer can be either negative or positive.]
- To visualize this, imagine an oscillating spring-mass system.
- If the body is displaced by x, then the acceleration will be a = -kx.
- If the body is displaced by -x, then the acceleration will be a = kx.
- As acceleration is the same magnitude but with a different sign for displacements of the same magnitude and opposite signs, velocity should also be the same.
- Thus with a displacement x, the velocity could be said to be v.
- With displacement -x, the velocity would be -v.
- The calculation for potential energy uses the formula for the potential energy for Hooke's law, where the constant k is substituted with angular frequency squared times mass.
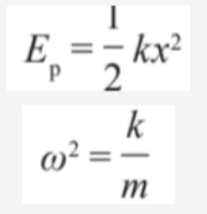
- As we can find velocity, we can also find kinetic energy at a any point by substituting velocity with its calculation.
- As energy is scalar, the positive or negative sign in the velocity function isn't important.
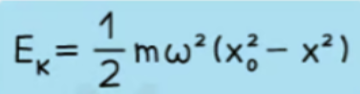
- Kinetic energy is at its highest when displacement, x is equal to zero, as then the potential energy is equal to zero, and all of the total energy consists of kinetic energy.
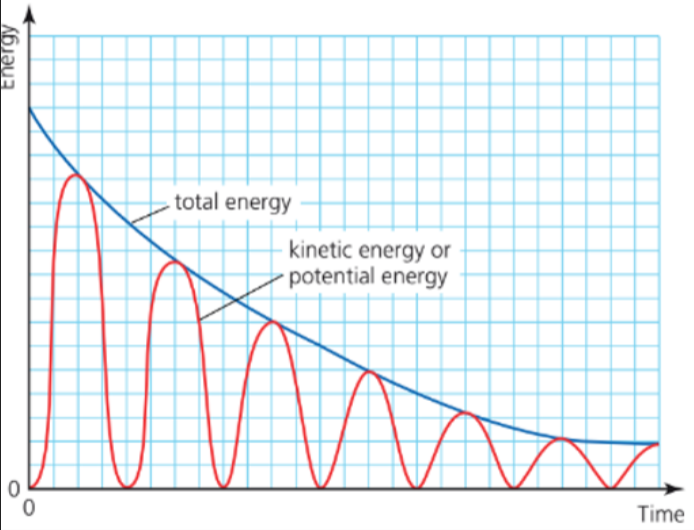
Damping
- In more realistic situations, the total energy will decrease over time as some of it is lost as it is transformed into heat and sound.
- The energy dissipation from an oscillating system is called damping.
- In the graph showing energy changes for simple harmonic motion, it will result in a gradual decrease.
Sources
https://circuityeldopinb.z21.web.core.windows.net/phase-shift-180-degrees.html