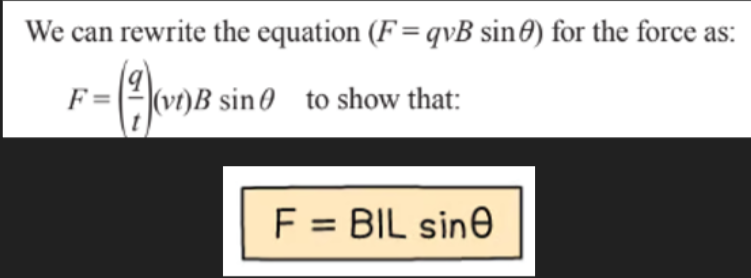Forces on Current-Carrying Conductors

Forces on Current-Carrying Conductors in a Magnetic Field

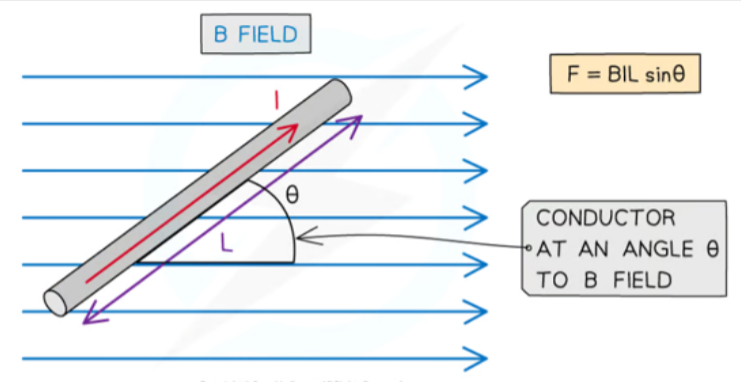
• We've discussed he magnitude and direction of the force on a current-carrying conductor in a magnetic field is given by F = BILsinθ.

• This equation is derived from the equation for the force on a charged particle moving through a magnetic field.

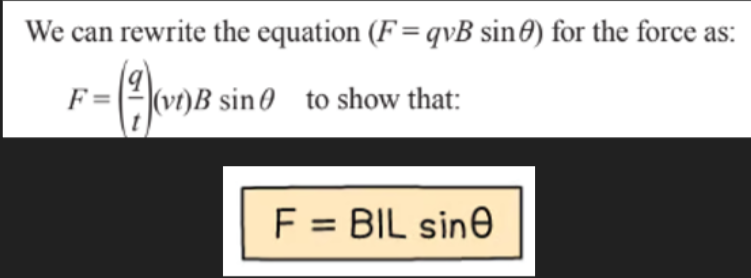
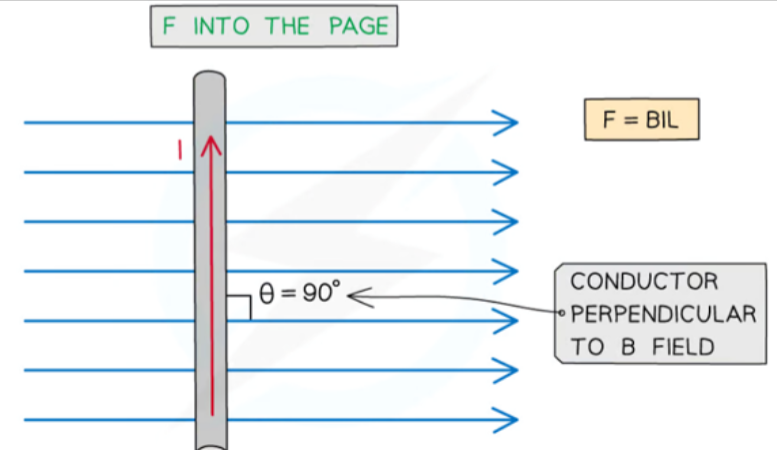
• The minimum force, F = 0N is when θ=0°, as then sinθ=0.
• This means that the conductor is exactly parallel to the magnetic B field.
• Thus a current-carrying conductor will experience no force if the current in the conductor is parallel to the field.
• This is because force, F, magnetic flux density, B, and the current, I, must be perpendicular to each other (recall the left-hand rule).

• The highest force is experienced when the conductor is perpendicular to the field, where θ=90°, as then sinθ=1.

Parallel Current-Carrying Wires

• Two parallel wires carrying a current will apply forces on each other.
• This is because each wire has a magnetic field around it, which the other wire is perpendicular to.

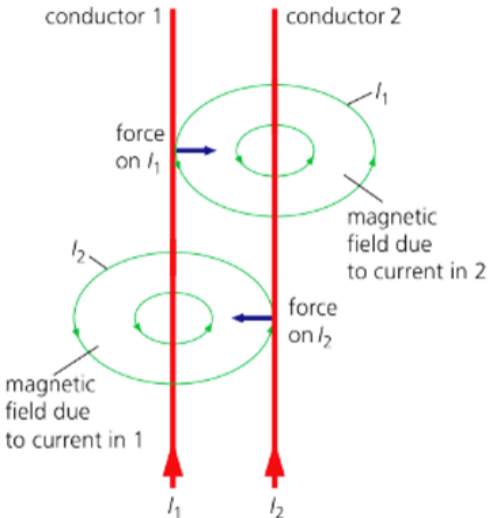
• The formation of the field depends on the direction of the current in the wires.

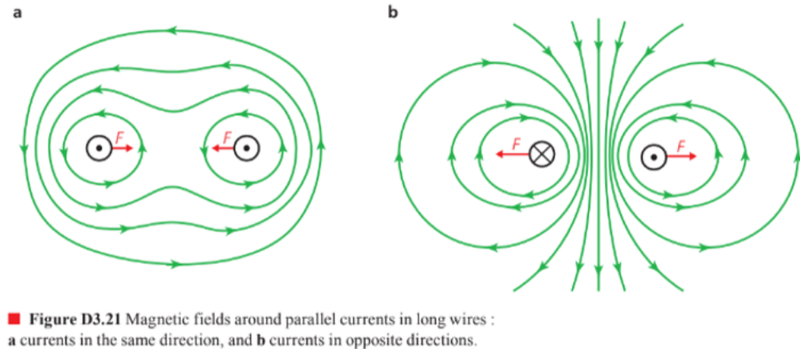
• Wires carrying the same direction current will attract each other and wires carrying currents of the opposite direction will repel one another.

• Current-carrying parallel wires will apply forces on each other for the entire length that the other wire is in their field.
• The force per unit length between parallel currents is given as:

• Where F is the force and L is the length of the wire.
• I is the current and r is the separation between the wires.
• μ₀ is the permeability of free space.