Entropy

What is Entropy?

• Entropy is often something you hear used in bad sci-fi movies, but in actuality it is a physical quantity.
• It is denoted as S, and is a thermodynamic quantity that relates to the degree of disorder of the particles in a system.
  • In simpler terms, it is the measure of how spread out or disorderly energy has become.

• Take for example, a heat engine.,
  • If the engine was being used to lift up a load we could say that if 100% efficient:
    • Internal energy -> Gravitational potential energy
  • However, this would never happen as the internal energy of a gas is random and disorderly whereas the gravitational potential energy of the load lifted up would be orderly.
  • Thus we can say that:
• It is not possible to increase the amount of order in a system.

Reversible and Irreversible Changes

• Processes can be organized into reversible and irreversible processes.

• A reversible process can be reversed so that the system and all of its surroundings return to their original states and there is no change in entropy.
  • Note that there is no external forces acting on the system.
• Reversible processes are an impossibility in the macroscopic world due to phenomena such as friction, fluids mixing, chemical reactions and electrical resistance which all increase entropy.

• Irreversible processes cannot be reversed.
  • Entropy always increases within irreversible processes.
  • All real macroscopic processes are irreversible.

• If the original state of a system and its surroundings can be restored exactly, the process is described as reversible.
• It can be considered that macroscopic processes in real isolated systems are almost always irreversible and consequently the entropy of real isolated systems always increases.
• Without outside interference, in any process, ordered energy of particles will be irreversibly transferred to disordered energy.

• Take, for example, a bouncing ball.

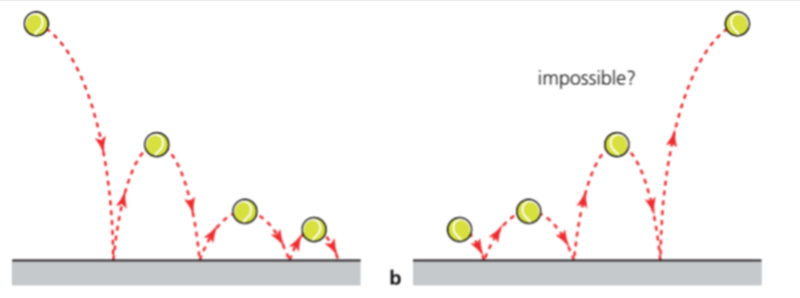
• As the ball bounces, part of its ordered gravitational potential energy is transferred into disorderly energy, such as heat and sound into its surroundings.
• Eventually the ball will come to a stop as all its energy is now disorderly.
• However, if the process were to be reversible, then the ball would be able to bounce back up to its original height, which should be impossible.

The Second Law of Thermodynamics

• The second law of thermodynamics refers to the change in entropy of an isolated system and sets constraints on possible physical processes and the overall evolution of the system.
• It shows that he entropy of a non-isolated system can decrease locally, but this is compensated by an equal or greater increase of the entropy of the surroundings.
  • In simpler terms, it states that:
    • In any cyclic process, the entropy will either stay the same or increase.

Examples of Entropy

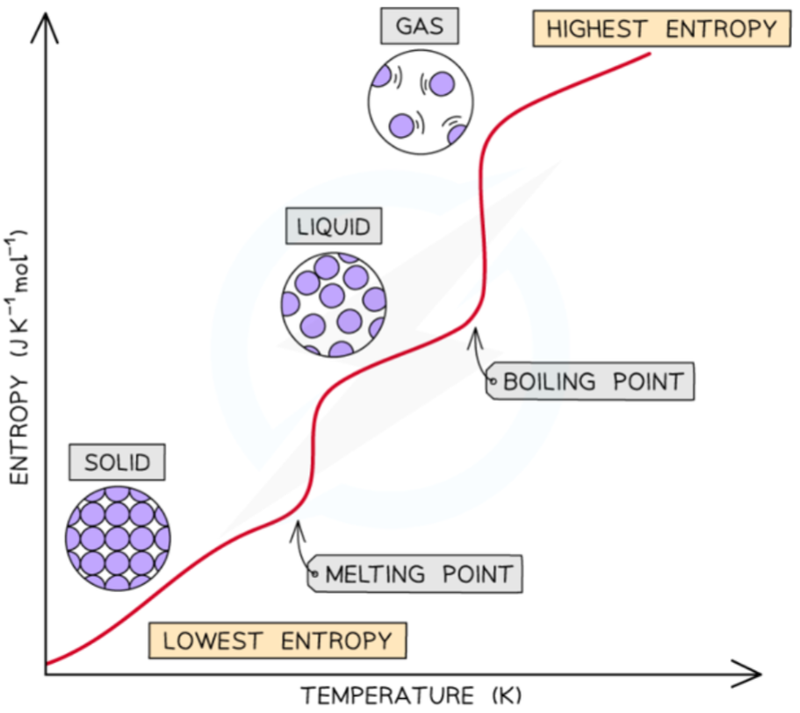
• Gas in a large volume is more disordered (greater entropy) than the same gas at the same temperature in a smaller volume.
• Gas at a higher temperature is more disordered (greater entropy) than the same gas at the same volume at a lower temperature.
• A liquid is more disordered (greater entropy) than a solid of the same material at the same temperature.
• Entropy can also increase when:
  • A solid dissolves in a solvent
  • A gas diffuses in a container

Entropy and Temperature

• As the temperature of a substance increases, the particles become more spread out and disordered, which means entropy increases.

Clausius Statement of the Second Law of Thermodynamics

• Recall the model for the heat engine.

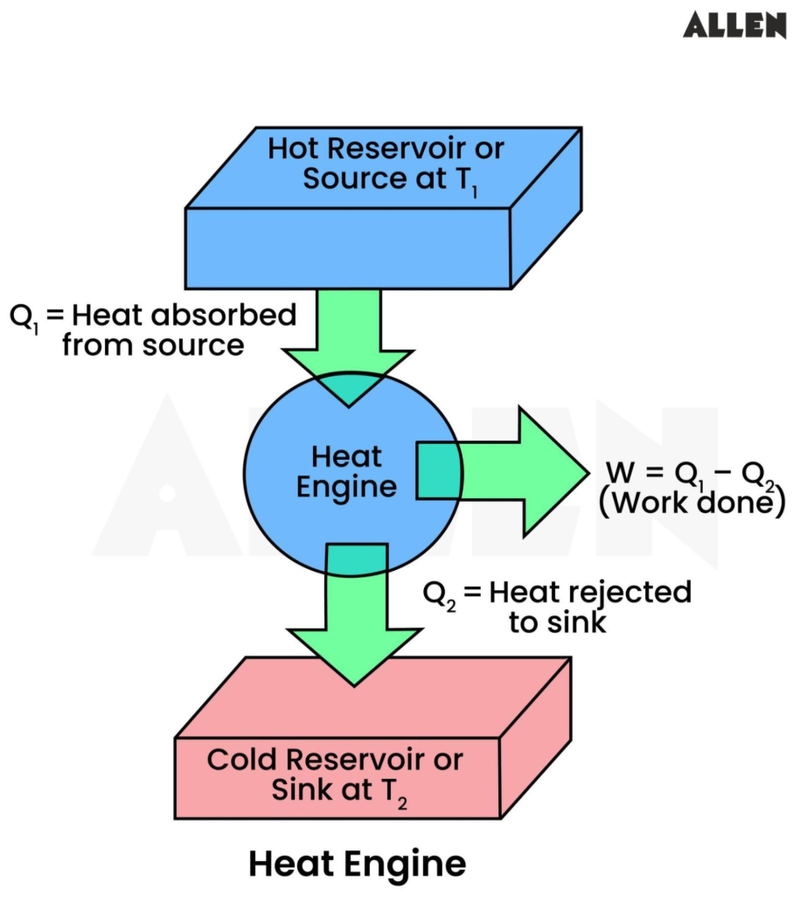
• To make energy go from the cold sink to the hot source we would need to put work in.
• Therefore it is not possible for heat to be transferred from a cold body to a warmer one without work being done.
  • However, work doesn't need to be done to transfer heat from a warm body to a cold one.

Kelvin-Planck Statement of the Second Law of Thermodynamics

• Recall the heat engine once more.I
• If the heat engine was being used to lift up a load and it was 100% efficient, then:
  • Internal energy -> Gravitational potential energy
• However, if we apply the second law of thermodynamics we see that:
  • It is not possible for a heat engine working in a cycle to absorb thermal energy and convert it all to work.

Entropy in Mathematical Terms

• Entropy can be determined in terms of macroscopic quantities such as thermal energy and temperature, as given by the formula:

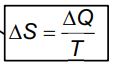
• Where ΔS is the change in entropy.
• ΔQ is the change in thermal energy of the system.
• T is the temperature of the system.
• From this formula we can see that entropy uses the units Joules per Kelvin.

Microstates

• Microstates are the numerous possible combinations of microscopic properties of a thermodynamic system.
• For a two-compartment container which holds N distinguishable particles, the number of microstates in the final volume is:
  • Ω = 2ᴺ
• Consider the general case of a system composed of N particles distributed among n boxes.
• The number of possible microstates for such a system is given as:
  • Ω = nᴺ

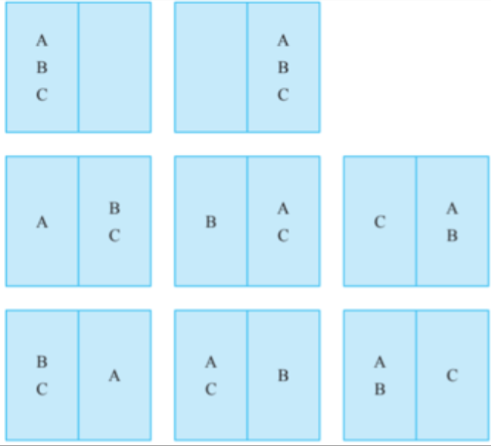
• Take for example, three particles A, B and C, arranged in two boxes.
• The possible arrangements would be:

Calculating Entropy of Particles

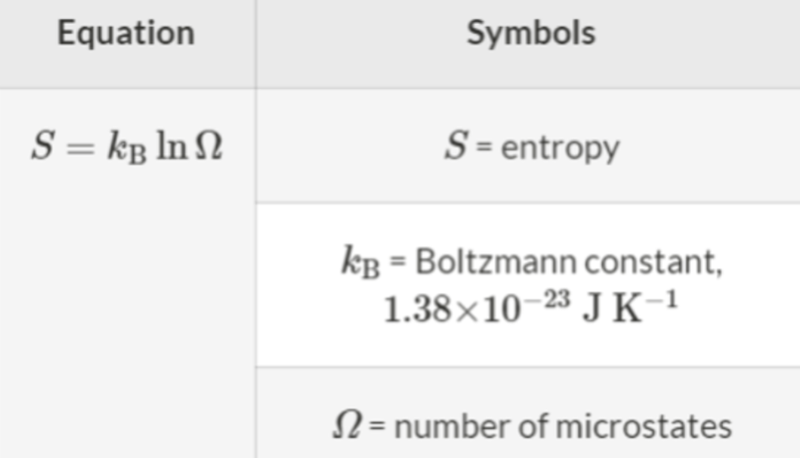
• Now that we know the definition of microstates, we can also define entropy in terms of the behavior of individual particles.

• Likewise, we can also use this formula for a change in the number of possible microstates.

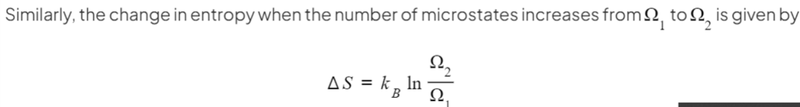
• This formula is derived from the previous one using logarithm rules.

Sources

https://www.youtube.com/watch?v=YsP4Jv8NtWY