What is Electric Potential
- Just like how a gravitational system has gravitational potential, a charge in an electric field has electric potential, Vₑ.
- However, electric potential has a fancy alternative name -you might have heard of it- it's called voltage!
- Electric potential is a scalar quantity with zero defined at infinity separation.
- Electric potential at a point is the work done per unit charge to bring a positive test charge from infinity to a point.
- The formula is given as:
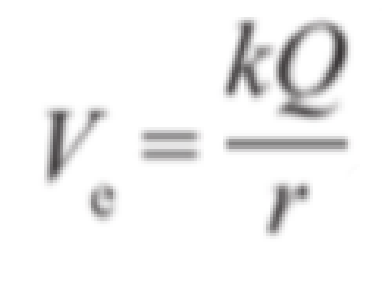
- Electric potential has the unit joules per coulomb, written as JC⁻¹.
- This is also simply given as volts, V.
1V = 1JC⁻¹
- The formula is derived from the formula for electric potential energy, by diving it with charge, just how the formula for gravitational potential is derived from gravitational potential energy by diving it with mass.
- Because we are dividing electric potential energy by charge, that means that electric potential must be always positive.
- You might have noticed a trend with the formulae of electric fields, where they are the same as the ones of gravitational fields, only with substituted values.
- The same holds true for electric potential, as it is the same formula as that for gravitational potential, only with the gravitational constant, G, replaced with Coulomb's constant, k, and mass replaced with charge.
Electric Equipotential Surfaces
- Electric equipotential surfaces are like gravitational equipotential surfaces.
- The electric potential is the same at all points on a particular circle.
- Moving between adjacent circles creates the same change in electric potential.
- Like gravitational equipotential lines, electric equipotential lines are always perpendicular to electric field lines.
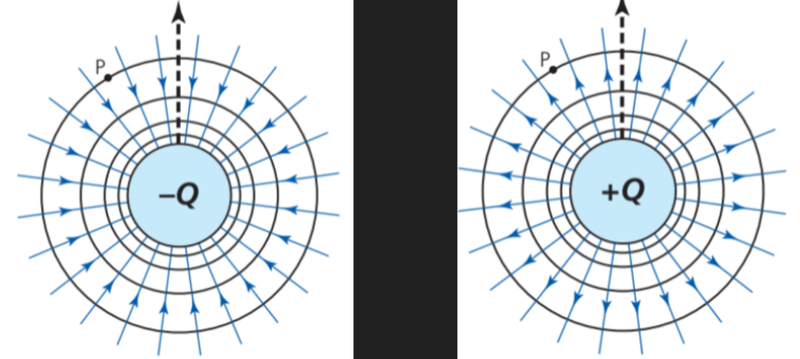
- Electric equipotential lines are drawn in 2 dimensions.
- If drawn in 3 dimensions, they are called equipotential surfaces.
- They will warp similarly to gravitational equipotential surfaces in different situations.
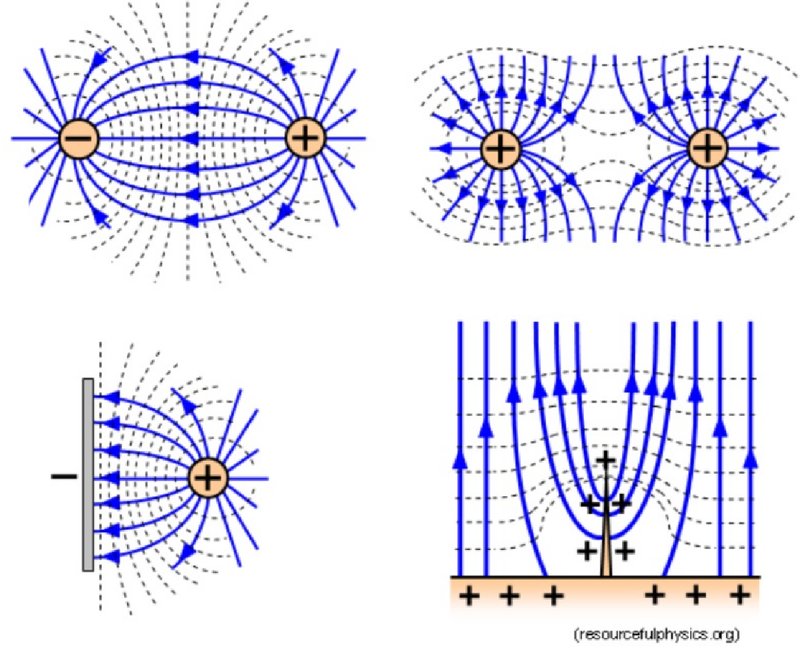
- In uniform electric fields, equipotential lines will form a neat little grid with the field lines.
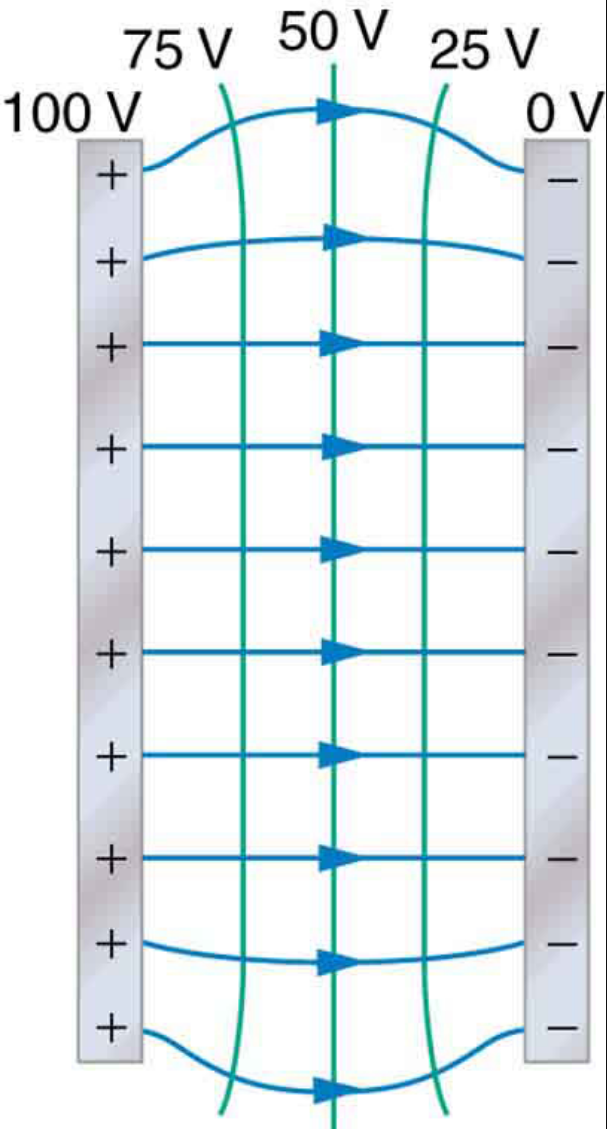
- In the above grid, we can see that moving back and forth causes changes in electric potential.
- Moving up and down, however, has no effect on electric potential!
Work Done
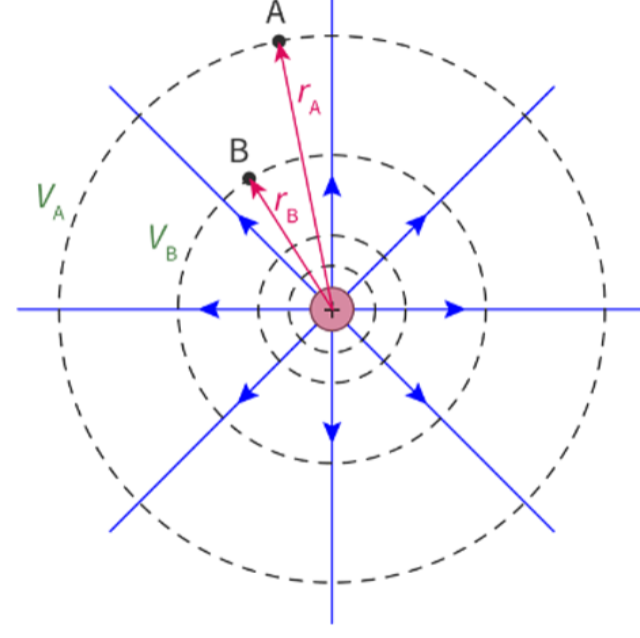
- Suppose that a charge is moved from point A to point B.
- This would result in an increase in electric potential, and likewise in electric potential energy.
- The work done would thus be the change in electric potential energy.
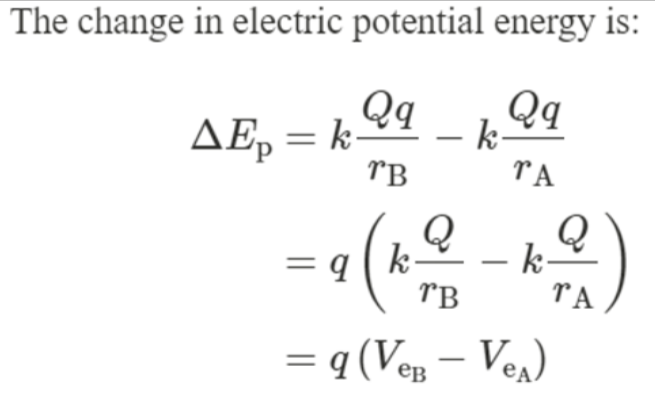
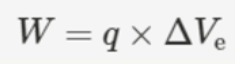
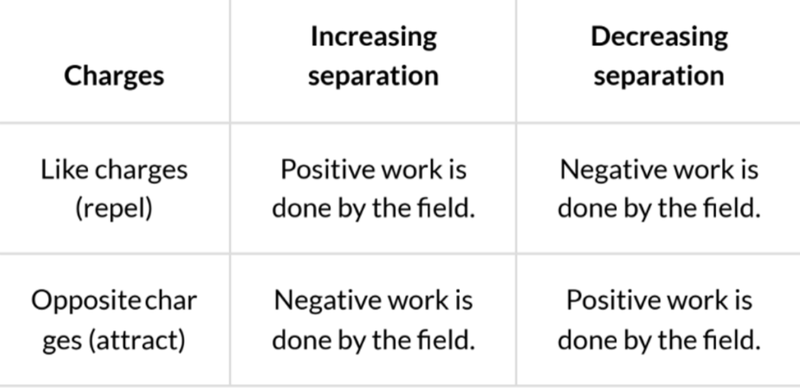
- The work done is thus equal to the product of the charge and the change in electric potential.
- This is similar to the work done in gravitational fields, which is the product of mass and change in gravitational potential.
Electric Field Strength in Terms of Electric Potential
- Recall how the derivative of gravitational potential with respect to separation was gravitational field strength.
- The same holds true for electric fields, and thus the derivative of electric potential is electric field strength, written as E.
- Electric field strength is thus given as:
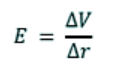
- And this can be rearranged into:

- From this formula we can see that, once again just like how gravitational field strength is equal to gravitational force divided by mass, electric field strength is equal to electrostatic force divided by charge, q.
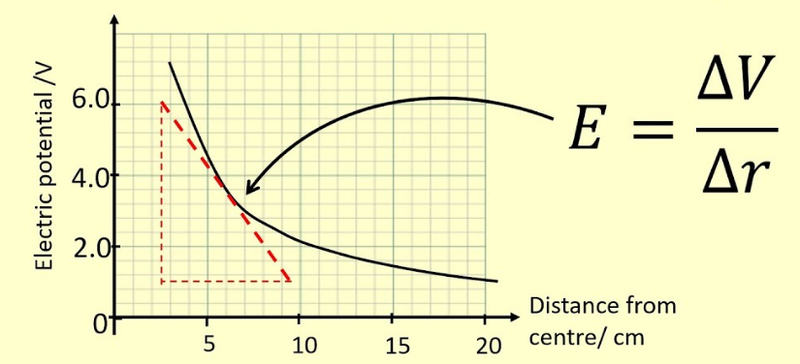
- As electric field strength is the derivative of electric potential, the gradient of a electric potential-separation graph is electric field strength.
- The area under an electric field strength-separation graph is the electric potential.
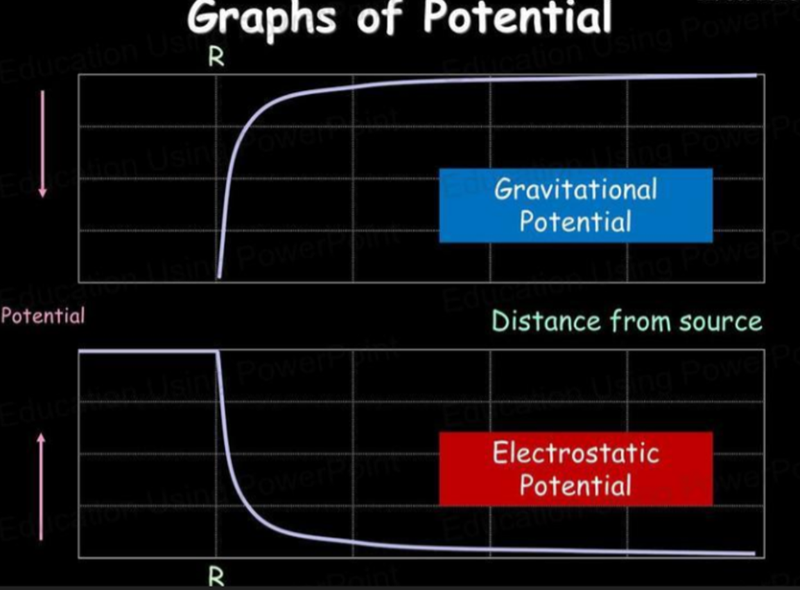
Electric Potential Graphs vs Gravitational Potential Graphs
Sources
https://philschatz.com/physics-book/contents/m42331.html