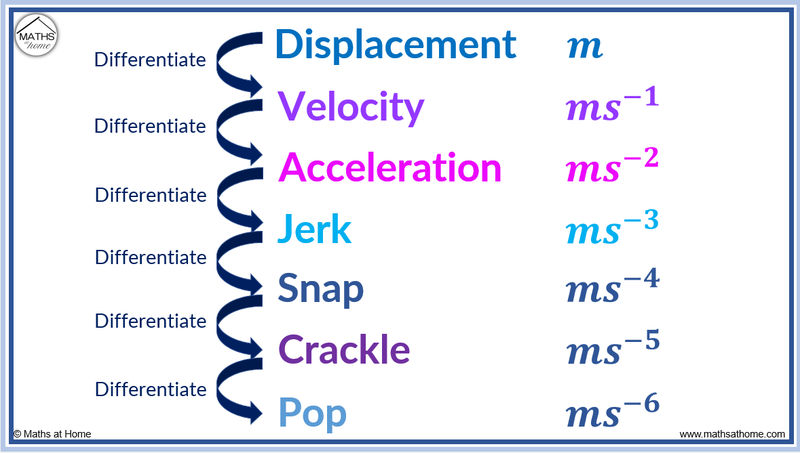
Velocity and Acceleration as Derivatives of Displacement
- Velocity is the rate of change of displacement, or the first derivative of displacement.
- Acceleration is the rate of change of velocity, or the rate of change of the rate of change of displacement.
- This means that acceleration is the derivative of velocity, or the second derivative of displacement.
- While velocity and acceleration are by far the most commonly used, displacement has far more derivatives, known as jerk, snap, crackle and pop, and are the 3rd, 4th, 5th and 6th derivatives of displacement respectively.
- Similarly, speed is the derivative of distance.
- The derivative of speed is called tangential acceleration, and like the other two values, it is scalar and thus only applies to one direction.
Motion Graphs
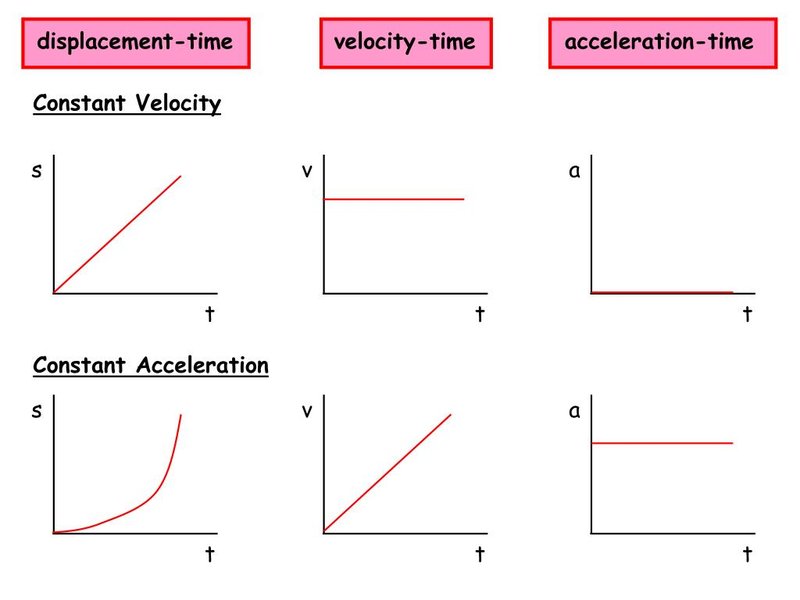
- As we discussed how acceleration and velocity are the derivatives of displacement, several details can be understood from their graphs.
- The gradient of a displacement-time graph represents velocity.
- The gradient of a distance-time graph represents speed.
- The gradient of a velocity-time graph represents acceleration.
- The gradient of a speed-time graph represents tangential acceleration.
- Similarly, these rules apply in reverse, as displacement is the integral of velocity, and velocity is the integral of acceleration.
- The area under a velocity-time graph is the change in displacement.
- The area under a speed-time graph is the distance travelled.
- The area under an acceleration-time graph is equal to the change of velocity.
Average Values
- Average speed is calculated as:
Average speed = total distance covered/time taken
- Average acceleration is calculated as:
Average acceleration = change in velocity/time taken
- Change in velocity is given by:
Change in velocity = final velocity - initial velocity
Δv = v - u
Uniformly Accelerated Motion
- Acceleration, denoted as a, is calculated as the change in velocity over the change in time.
- For motion that is uniformly acceleration, velocity increases at a constant rate, and therefore the following formulae can be used to find acceleration:
a = Δv/Δt
a = (v-u)/Δt
- Where Δt is the change in time and Δv is the change in velocity.
Instantaneous Velocity
- The instantaneous speed (or velocity) is the speed (or velocity) of an object at any given point in time.
- To find the instantaneous velocity on a displacement-time graph, you have to draw the tangent at the specific point on the graph, and then calculate the gradient of the graph, which will give you the velocity at that instant.
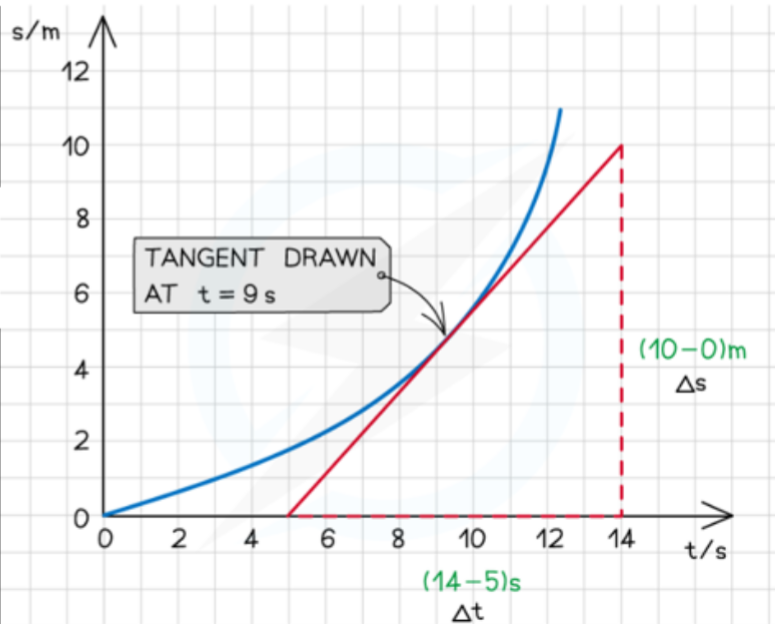
- Alternatively, you could find the derivative of the graph, and then replace the value for time with the specified time.
Sources