Position
- In order to describe how objects move, we need to know and understand their positions.
- The easiest way to determine this is by drawing the objects on a coordinate grid.
- Their position can be described according to a certain reference point.
- For example an objects position could be (-3, 4) from a zero point. By plotting those coordinates down in a grid with the axes along the cardinal directions (x-axis is east and west and the y-axis is north and south) it becomes easy to tell that the object is three units to the west and four units to the north.
Change in Position
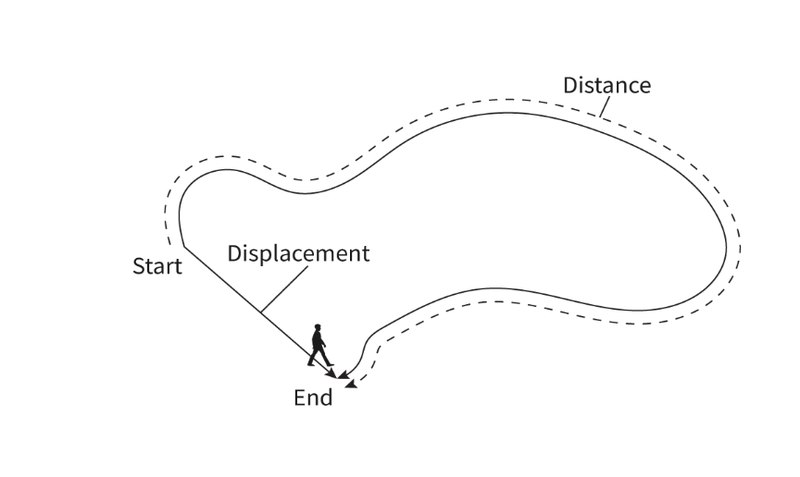
- There are two distinct measurements that tell us about change in position.
- They are displacement (x) and distance (s).
Distance
- Distance is generally what you think of when you think of change in position.
- Distance is a scalar quantity, meaning it doesn't have a direction.
- It describes the entire path taken to reach a position.
- For example if you drive a car to the grocery store which is 4 kilometers away, your distance might be around 5 kilometers due to all the twists and turns you will have made along the way.
Displacement
- Displacement describes the change in position from one point to another in a straight line.
- Distance is a vector quantity.
- Displacement does not account for changing of paths.
- For example if you took the same trip in your car to the grocery store, while your distance might be 5 kilometers or more, your displacement would only be 4 kilometers.
- Likewise, if you go on a bike trip and travel 5 kilometers away from your home and make the same trip back, your distance traveled would be 10 kilometers. However, your displacement would be 0 kilometers as you'll have ended up in the same position as you started!
Velocity and Speed
- Similarly, velocity and speed are two vector and scalar quantities that describe similar phenomena.
Speed
- Speed is a scalar quantity and it's written as distance divided by time.
- It can be described as change in distance over change in time.
- It only has a magnitude.
Velocity
- Velocity is a vector quantity that is written as displacement divided time.
- It can be described as change in displacement over time.
- Velocity has both a direction and a magnitude.
Acceleration
- Acceleration is the increase or decrease in an object's velocity.
- It is a vector quantity that measures the change in velocity over change in time.
- This means that acceleration measures the change in displacement over change change in time over change in time.
- Thus it can be written as meters divided by seconds squared, or ms⁻².
- Acceleration can be positive or negative, depending on the change in velocity.
- For example if you slow down by 5 m/s then the change in velocity is -5 ms⁻¹
Positive Direction
- An object with increasing velocity in the positive direction has positive acceleration.
- An object with decreasing velocity in the positive direction has a negative acceleration.
Negative Direction
- An object with decreasing velocity in the negative direction has positive acceleration.
- An object with increasing velocity in the negative direction has a negative acceleration.
Graphs of Motion
- Graphs can describe the motion of an object.
- A time-displacement graph shows how the displacement of an object changes over time.
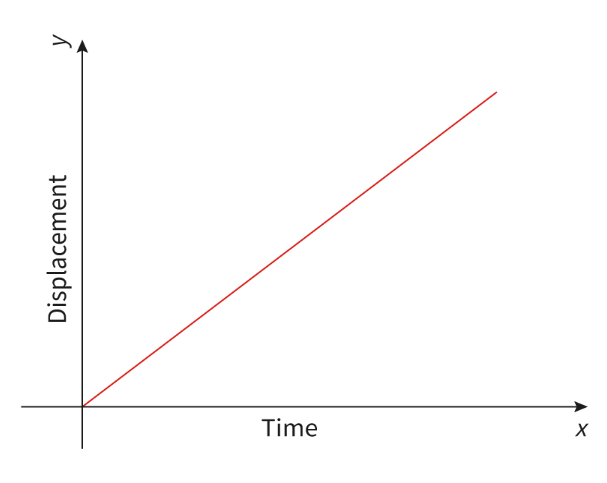
- The gradient of a line gives you the rate of change.
- For example a gradient of 3 for a time (seconds) displacement (meters) chart would mean that the rate of change is 3 meters of displacement every second.
Finding Components of Graphs
- Creating shaded areas can help us find certain components of the graph by calculating the area.
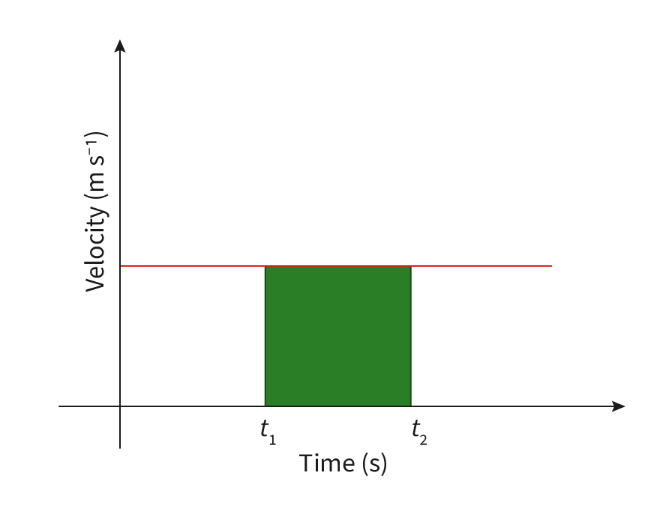
- The green area shows displacement as velocity (m/s) multiplied by time (s) gives meters.
Average Values
- Throughout a time frame, velocity can vary, thus the average can be found by dividing the total displacement by the total time spent.
Instantaneous Values
- Instantaneous values can be found from graphs.
- In a graph with a constant gradient (straight line), instantaneous values can be found by locating any point on the line. Thus the gradient is the value.
- However graphs aren't always constant (curved line).
- In this scenario a tangent line should be drawn based on a point in the graph.
- Calculating the gradient of this tangent line gives us the instantaneous value for that point.
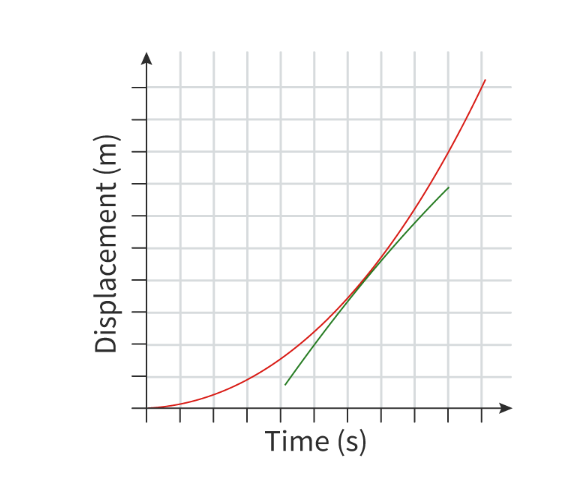
Uniform and Non-Uniform Acceleration
- Motion can either have no acceleration, meaning that the velocity is constant, uniform accelerating, meaning that velocity constantly increases, or non-uniform acceleration, meaning that the velocity increases or decreases varyingly.
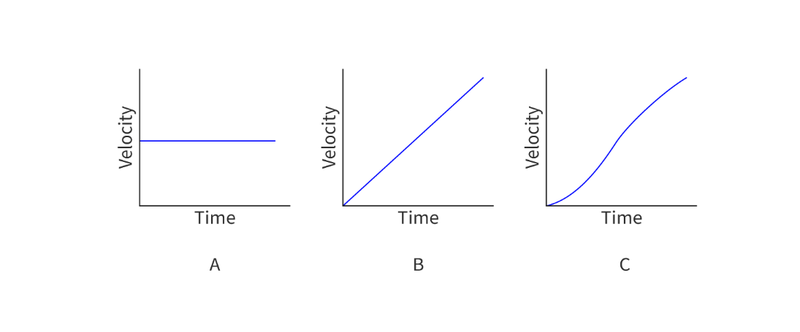
- In the picture above, A represents an object with no acceleration, B represents an object with uniform acceleration and C represents an object with non-uniform acceleration.
Image Sources




