The Principle of Conservation of Energy
- The principle of conservation of energy states that energy cannot be created or destroyed, but only transferred from one form to another.
- Hence, for an isolated system, the sum of the useful and wasted energy outputs will always be equal to the total energy input.
- In the absence of resistive forces, the total mechanical energy of a system is conserved.
- If mechanical energy is conserved, work is the amount of energy transformed between different forms of mechanical energy in a system, such as kinetic energy, gravitational potential energy and elastic potential energy.
Using Conservation of Energy for Falling Objects
- While we're used to using SUVAT equations for calculating the speed and height of falling objects, energy conservation can also be applied to these situations.
- Imagine a ball being thrown upwards.
- At the very moment it is thrown, its height, and therefore gravitational potential energy is equal to zero, and its kinetic energy is at the maximum value.
Example
- Imagine a bouncing ball. With each bounce, the ball rises and loses kinetic energy as it gains gravitational potential energy.
- As it bounces, some energy is lost due to it being dissipated as heat and sound.
- What the graphs will look like are shown below:
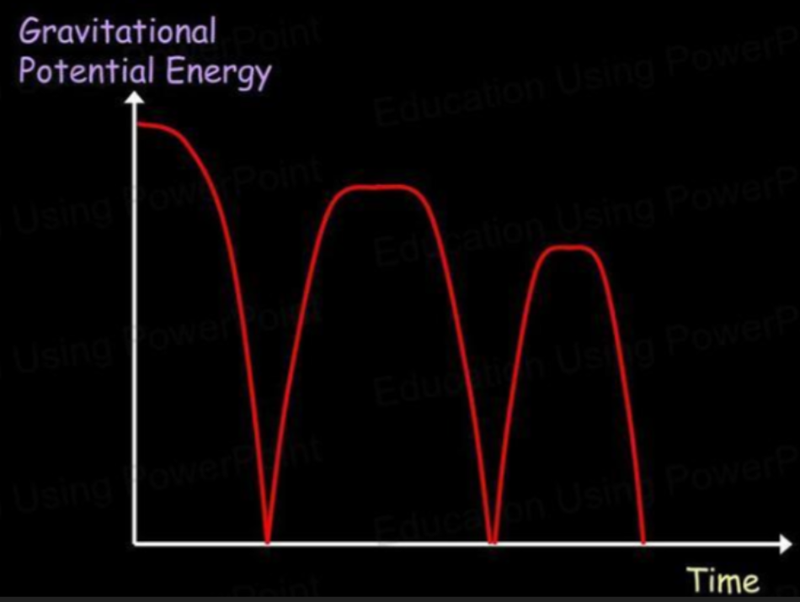
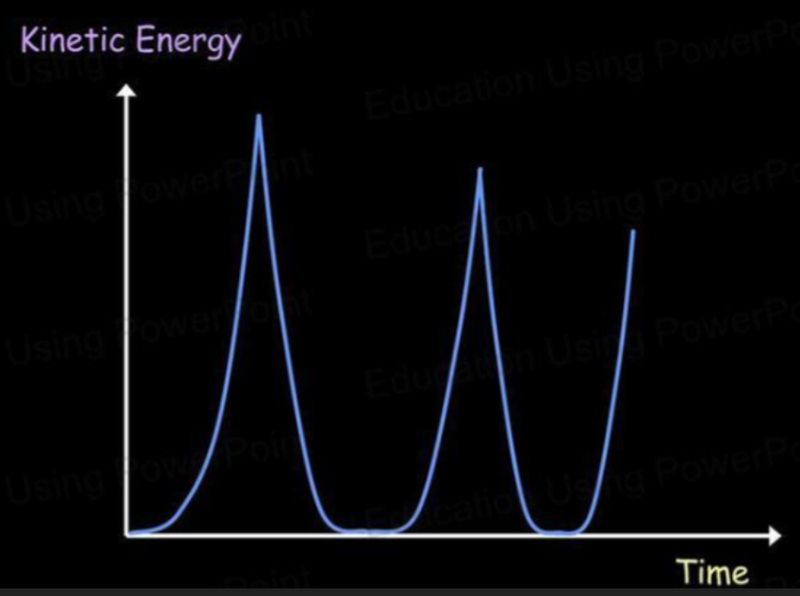
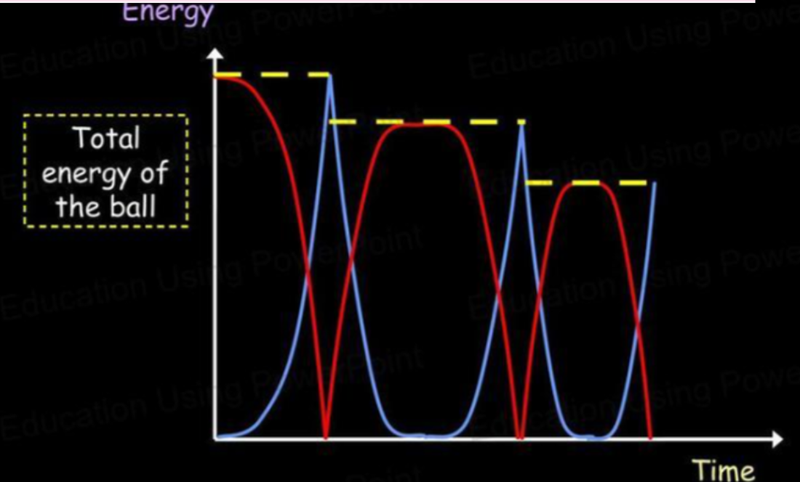
- Notice how both graphs have their maximum points at the same amount of energy.
- As one graph increases, the other decreases.
- Thus at the maximum point of the kinetic energy graph, gravitational potential energy is zero.
- Likewise, at the maximum point of gravitational potential energy, kinetic energy is zero.