What is Circular Motion?
- Circular motion, as evidenced by its name, is when an object moves in a circular path, often in repeating cycles.
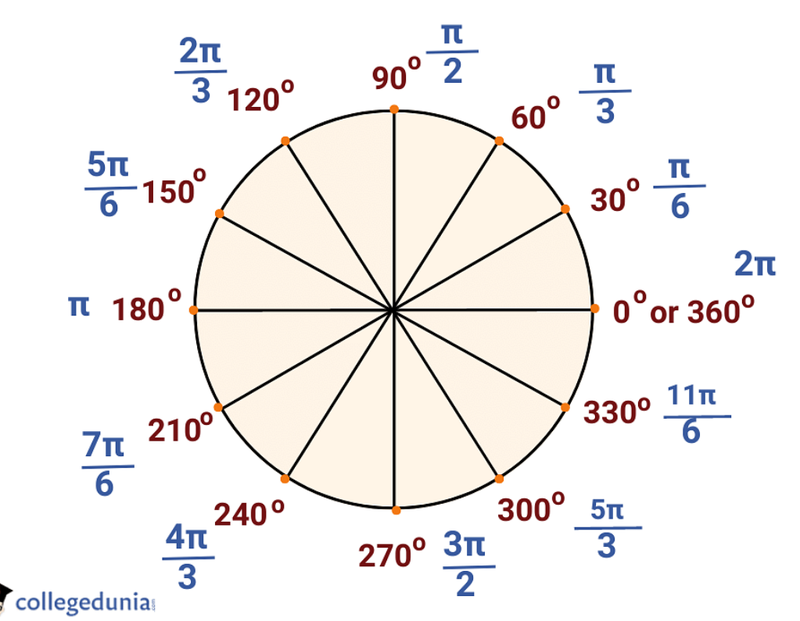
Radians
- Circular motion relies primarily on radians, rather than degrees, to find angles.
- Radians are an alternative way to describe angles, and are found by dividing the arc length of the angle by the radius.
- The measures of angles in radians are:
Features of Circular Motion
Position
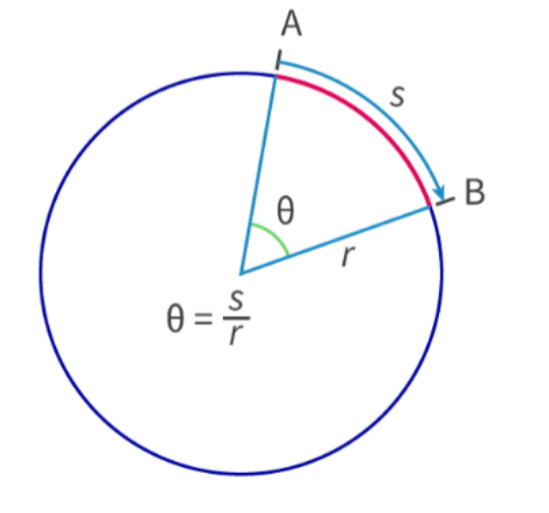
- As radians are determined as θ = s/r where r is the radius and s is the arc length of the angle, the position on the circular path can be determined by s = rθ.
Period
- The period is the time taken to cover one complete circle.
- It is denoted as T and uses the unit seconds (s).
Frequency
- Frequency, f , is measured in Hertz (Hz) and describes the number of complete revolutions made in one second.
- Frequency and period are by definition reciprocals of one another.
- Thus:
f = 1/ T
T = 1/ f
Speed
- As speed has no direction, and is simply the distance an object covers over time.
- As in circular the change in time is Δt = T when a body completes one full circle ,2πr; the average speed during circular motion can be calculated as:
2πr/ T = v
- Where v is speed, and 2πr is the circumference of the circle, therefore being the distance covered.
Angular Velocity
- Angular velocity, ω, is written in the units radians per second, and shows the rate of change of the angle covered in an amount of time.
ω = θ/Δt
- Angular velocity can be determined when the body completes one circle and the change in time is one period.
θ = 2π
Δt = T
Therefore:
ω = 2π/ T
- As speed is equal to 2πr/ T, then angular velocity must be:
v = ωr
- As long as the speed is constant, and the radius is constant, then angular velocity will be constant as well.
- In circular motion, speed and angular velocity function most closely to linear velocity/speed.
Angular Acceleration
- Angular acceleration, α, describes the rate of change of angular velocity.
- If an object speeds up or slows down during circular motion, then the angular acceleration does not equal zero.
- It can be described in several different ways:
α = ω/Δt
α = v/(r*Δt)
Tangential Velocity
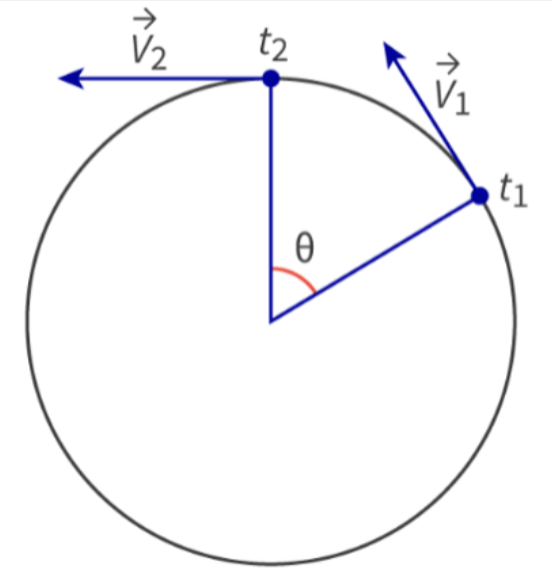
- However, when an object is moving in a circle, it is constantly changing direction as it turns inwards.
- This is described by tangential velocity, vₜ, and it shows the linear velocity of an object at any point during circular motion.
- The vector for tangential velocity will always be tangent to a point on the circular path.
- As linear speed, which is independent of direction, is described as v = ωr, then tangential velocity, which shows linear velocity can be described in the same way.
vₜ = ωr
- Except this time, tangential velocity is constantly changing direction.
Tangential Acceleration
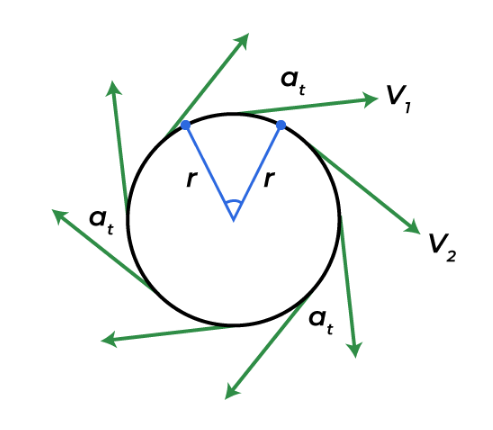
- Tangential acceleration, aₜ, describes the rate of change of tangential velocity.
aₜ = vₜ/Δt
- Tangential acceleration however, is independent of direction and is scalar.
- This is because, as tangential velocity is changing direction all the time, tangential acceleration is also changing direction at the same rate.
- Tangential acceleration thus only considers the change in magnitude of tangential velocity.
Centripetal Acceleration
- However, even if tangential acceleration is zero, the tangential velocity is still constantly changing direction, indicating that there must be some other acceleration
- This is the centripetal acceleration!
- Centripetal acceleration is always towards the centre of the circle and thus it is always normal to tangential velocity.
- Every type of circular motion needs centripetal acceleration to keep the body from straying out of path.
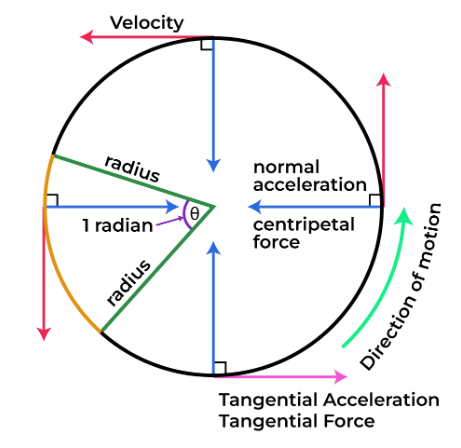
- Centripetal acceleration can be defined by two different formulas:


Centripetal Force
- Considering there is a centripetal acceleration, there must be a force pulling an object inward to accelerate it.
- This is the centripetal force.
- Centripetal force is not a unique type of force like gravity or tension.
- Instead, any force that pulls an object inward and causes circular motion is called a centripetal force.
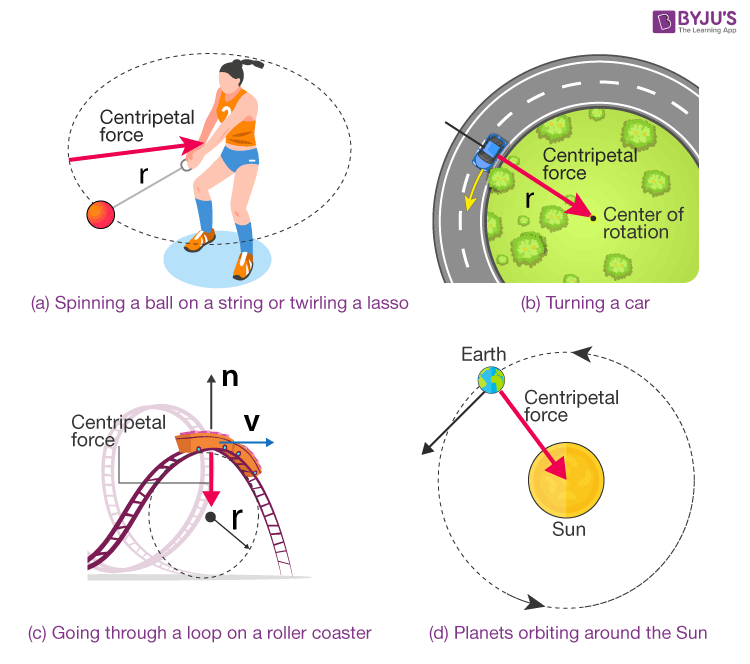
- For there to be circular motion, the centripetal force has to be great enough so that a = v²/r or a = ω²r.
- As force is defined as F = ma, the force can be found by substituting the acceleration with the centripetal acceleration.
- Therefore centripetal force is defined as:

- If the force is too little or too much then the object will go off course.
Centrifugal Force
- Centrifugal force is considered a fictitious force, as it only exists if there is a centripetal force at play.
- It is in the opposite direction to centripetal force and is equal to it.
- This means it can be calculated in the same way as centripetal force.
- Centrifugal force disappears the instant there is no longer a centripetal force.
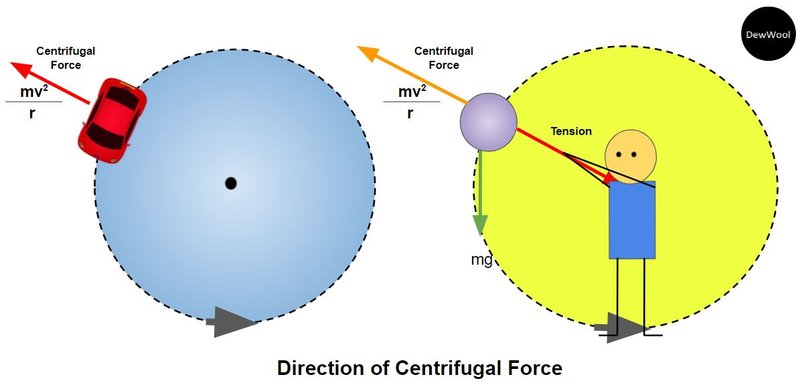
- While centrifugal force isn't important when it comes to understanding circular motion, it has some niche real-world applications.
- The most important thing is to not get it confused with centripetal force!
Vertical Circular Motion
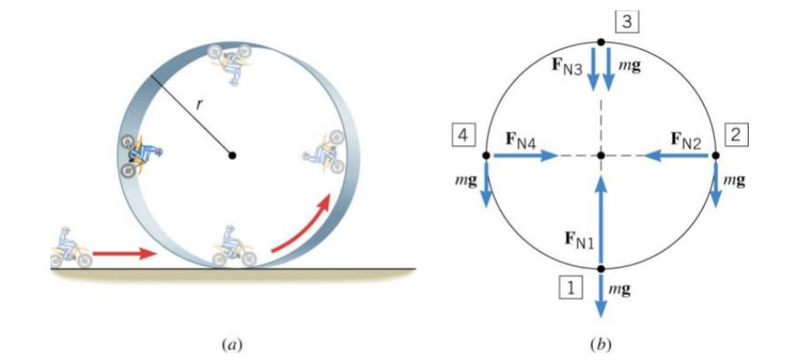
- During circular motion, the effect of gravity changes the composition for the centripetal force.
- Assuming angular velocity is constant, the centripetal force should also stay constant.
- However, the forces that make up the centripetal force are different at different positions.
- For example, for a bike going around a loop, at the top the centripetal force is equal to Fc = Fₙ + Fg.
- At the sides it is Fc = Fₙ
- At the bottom it is Fc = Fₙ - Fg
- This means the normal force will be strongest at the bottom and the smallest at the top.
- The same applies to other situations, such as a ball being swung around vertically on a rope.
- Except in this situation, the normal force, Fₙ, is replaced with the tension force in the rope, Fₜ.
Sources
https://www.geeksforgeeks.org/tangential-acceleration-formula/
https://byjus.com/physics/centripetal-and-centrifugal-force/
https://vmtery.weebly.com/blog/circular-motion
https://www.examples.com/physics/centripetal-force-formula.html
https://dewwool.com/centrifugal-force-definitionexamplesformula/