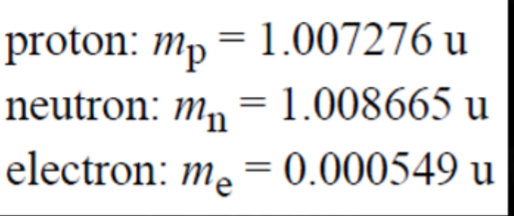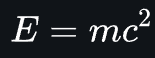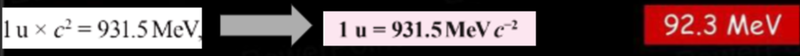Binding Energy

Unified Atomic Mass Unit

• The unified atomic mass unit, u, is used to measure the mass of atoms relative to one another.
• The mass of a single carbon atom is approximate 1.99*10^-26kg.
• As carbon-12 has 12 nucleons, 1 nucleon must be 1/12th of that mass.

• According to a periodic table, the relative atomic mass of hydrogen is 1.0079.
  • This means its mass is m = 1.0079u, or 1.67*10^-27kg.

Binding Energy

• Consider a carbon-12 atom again.
• It has 6 protons, 6 neutrons and 6 electrons.

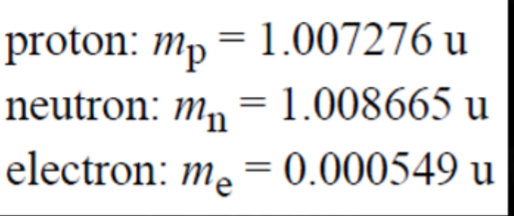
• Clearly a carbon-12 atom has a mass of 12u.
• The actual mass of the carbon nucleus can be calculated as:

• However, if we add up the mass of 6 neutrons and 6 protons, we get something different!

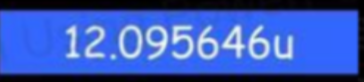
• This is strange! There's a difference between the defined mass using the unified atomic mass unit and the measured mass by adding up protons and neutrons.

• Has physics failed us? Not quite!
• This difference is called the mass deficit and it exists because some of the mass is in the form of energy that keeps the nucleus together.
  • This is called the binding energy of the nucleus.
  • It can be alternatively defined as:
    • The amount of energy needed to completely separate the nucleons.
    • The energy released when a nucleus is formed from nucleons.

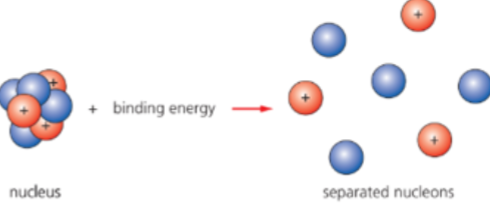
• The binding energy BE is measured in the megaelectronvolt, MeV.
• Binding energy increases as the number of nucleons in the nucleus increases, because it requires more energy to separate more nucleons.

Energy-Mass Equivalence

• Energy being in the form of mass might be strange, but it brings us to the most famous formula in physics:

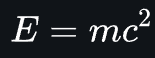
• This equation shows that mass is just another form of energy.
  • While speculated on before several times, Albert Einstein was the first to properly deduce this formula.

• It can also be given in the form of atomic mass units.
• If an object gains energy its mass increases ever so slightly.
  • However, the change is far too small to detect.
• Mass is the energy an object has because of the matter it is made of.
  • It is hidden energy.

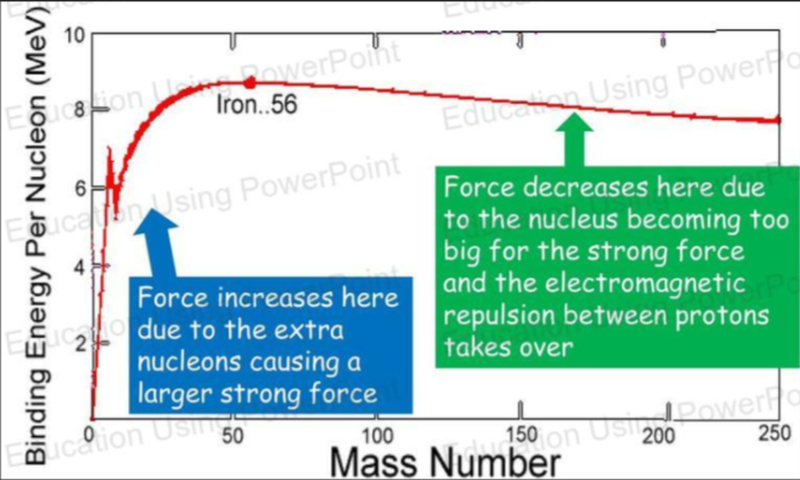
Binding Energy Per Nucleon

• Using the energy-mass equivalence formula, and the mass of the binding energy for carbon-12, we can work out that each carbon-12 nucleus has a binding energy of 1.48*10^-11J.
• Calculating this in eV gives us:

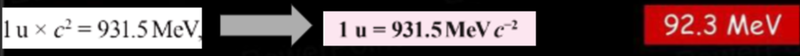
• The binding energy per nucleon is calculated as 7.68MeV.
• That means we can calculate binding energy per nucleon as:

• The A here is the atomic number, not to be confused with activity.
• Binding energy per nucleon tells us how strongly each nucleon is held together.

The Energy Inside a Nucleus

• How is the mass defect of a nucleus related to its binding energy?
• Consider nucleus B with a large mass defect:
  • The mass of the nucleus is much less than the mass of its separated nucleons.
  • The energy of the nucleus is much less than the energy of its separated nucleons (since mass is energy.
  • To separate the nucleus into its nucleons, the amount of energy in B would need to be supplied as work.
  • The nucleus has a large binding energy (equal to the energy in B).
  • The nucleus is difficult to separate into its individual nucleons.
    • This difficulty in separating nucleons means it is more stable.