What is Angular Momentum?
- Just like how any object with a mass and linear velocity has linear momentum, any object with inertia and angular velocity has angular momentum.
- Angular momentum is written as L, and is calculated as:
L = Iω
- Where:

- Just how linear momentum is always conserved, angular momentum is also conserved.
- This means that the angular momentum of an isolated system always remains constant.
Example
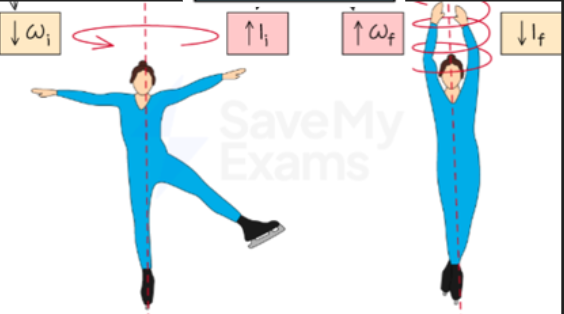
- If an ice skater spins around with her arms out, she has a higher moment of inertia, this means her angular velocity will be quite slow.
- However, if she tucks her arms in, her moment of inertia gets smaller.
- This would result in a decrease in angular momentum, which cannot happen, so to compensate, angular velocity increases and she starts rotating faster.
Torque and Angular Momentum
- However, if torque is acting on a system, just how force causes a change in linear momentum, there is a change in angular momentum.
- We went over how torque is defined as τ = Iα.
- And as α = ω/Δt, this means that torque can be redefined as τ = (Iω)/Δt = L/Δt.
- Therefore, just how force is the rate of change of momentum, torque is the rate of change of angular momentum.
- And whenever something is the rate of change of something, it means that it is the derivative of that thing!
- Therefore, the gradient of an angular momentum-time graph is torque, and the area underneath a torque-time graph is angular momentum.
Transfer of Angular Momentum
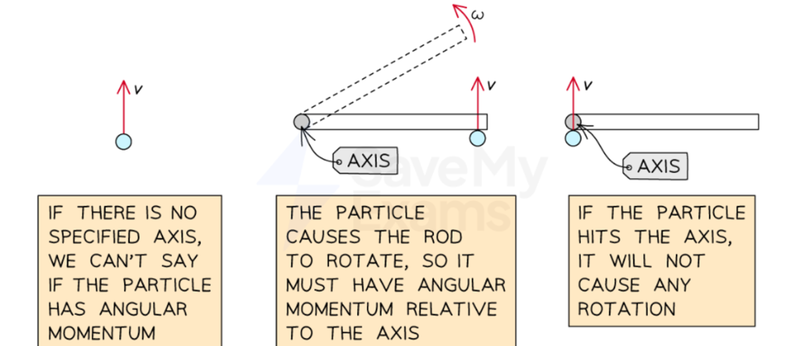
- As a moving particle has energy, if it impacts an object on an axis, then that energy can be transferred to it as torque.
- This leads to the object on the axis gaining some angular momentum.