Examples of Functions
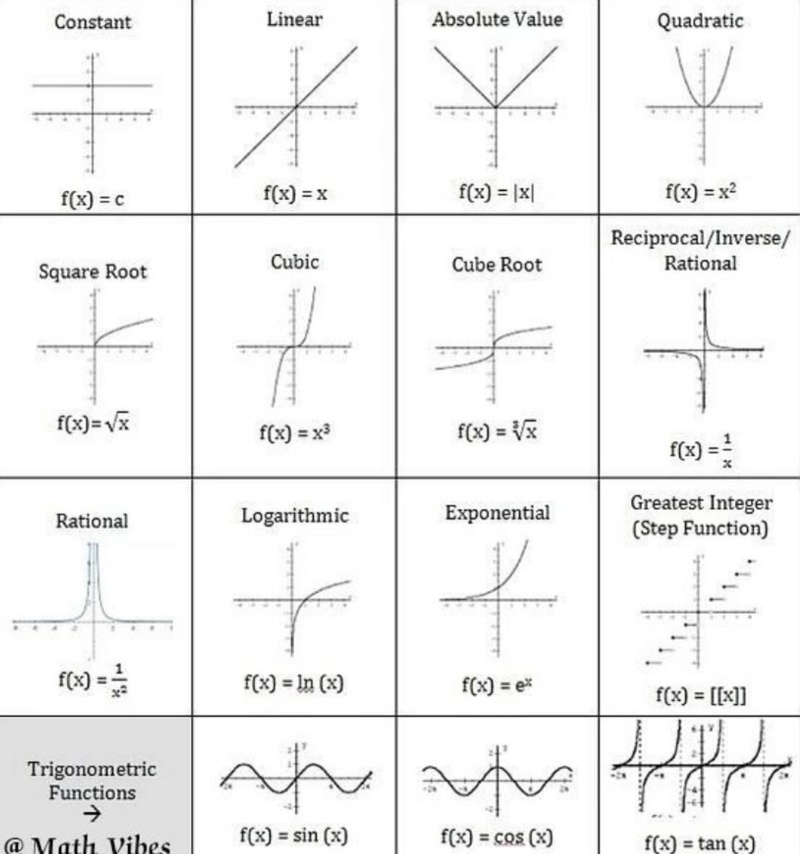
Constant Functions
- Constant functions are straight lines.
- While only y = c, where c is a constant is a function, you might also see a vertical line x = c.
- However, x = c is a relation.
Linear Functions
- Linear functions are simply a straight angled line.
- They have a constant gradient and are expressed as y = mx + b.
- m determines the gradient and b shifts the function up or down.
- A line perpendicular to a straight line always has gradient -1/m.
Modulus Functions
- Modulus, or absolute value functions take the distance of x from zero, meaning it does not matter whether the value is positive or negative.

- Modulus functions will "bounce back" at the x-axis, so that the part that would normally be below the x-axis is flipped relative to it.
- However, if only the absolute value of x is taken, then the function is mirrored around the y-axis instead, as they will give the same results as if the function were in the positive side.
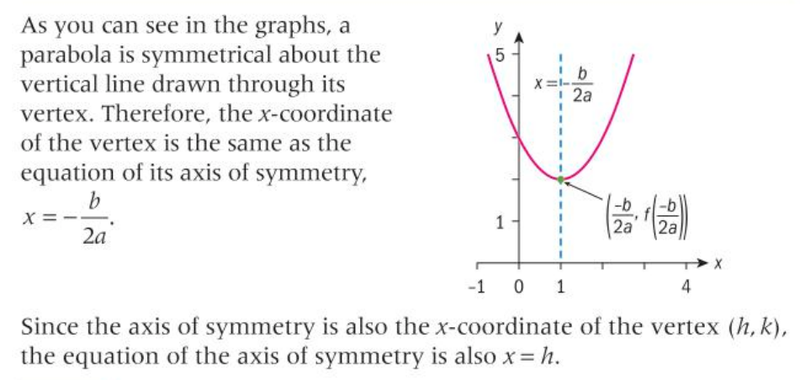
Quadratic Function
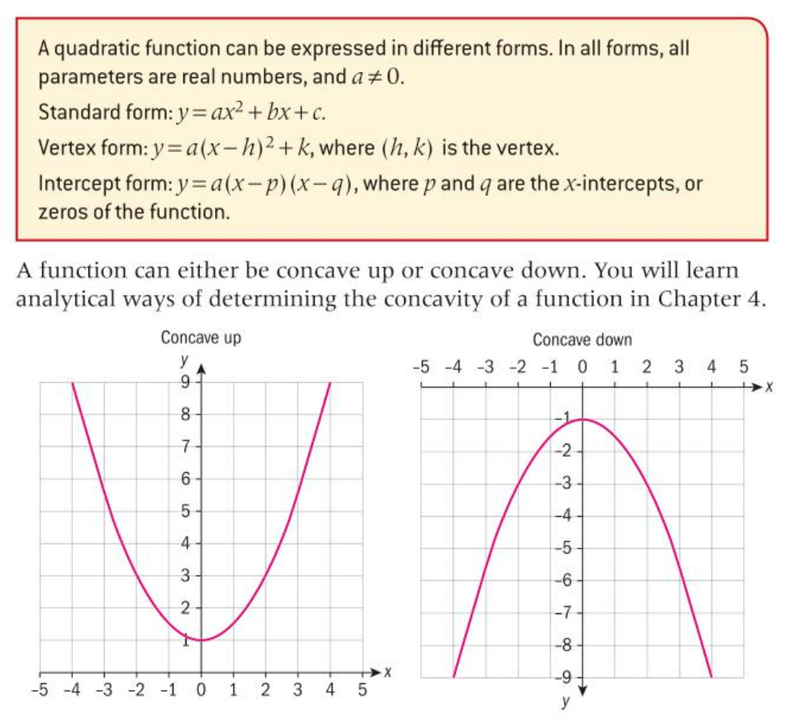
- A quadratic functions contains a value of x² as the highest degree and take the shape of a parabola.
- A function can either be concave up or concave down.
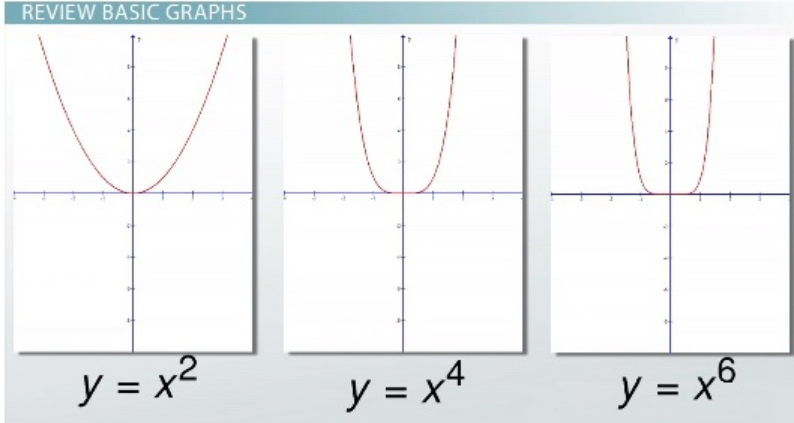
Cubic Function
- A cubic function contains an x³ as the highest degree and it resembles a rotated "s" shape.
- Powers higher than x³ will alternate between being shaped like an s and a parabola.
- Even numbers are shaped like a parabola and odd numbers are shaped like an s.
- With increasing power, the curve of the function will get more and more angular.
Square Root Function
- A square root function contains √x.
- This results in a rotated parabolic function.
- Yet the function cannot go below zero, as then it would be a relation.

Cubic Root Function
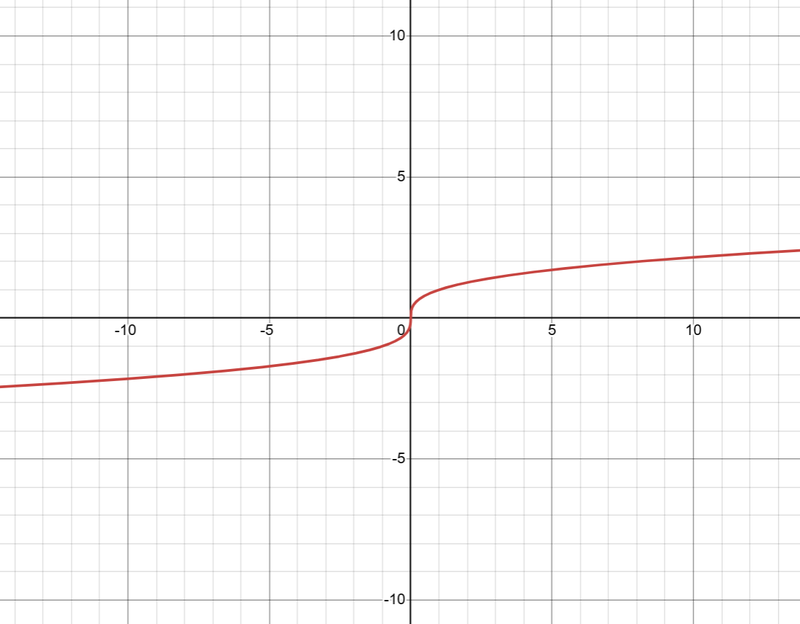
- A cubic root function contains a cubic root of x, ³√x.
- Just like how a square root function is a rotated quadratic function, a cubic root function is a rotated cubic function.
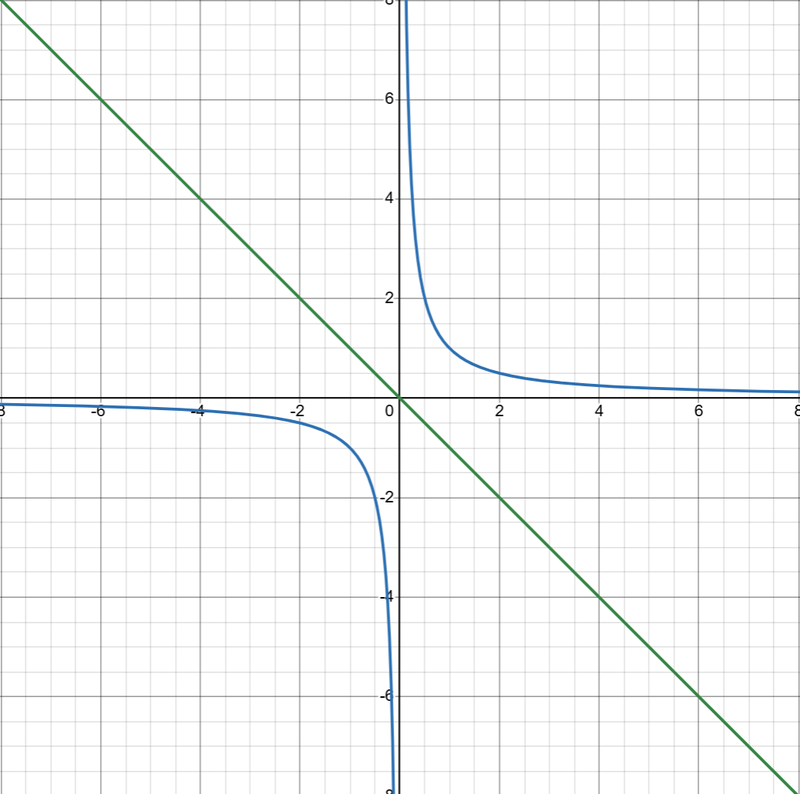
Reciprocal Function
- The reciprocal function, y = 1/x is a type of rational function.
- It is also called a hyperbola.

- The domain includes all values except for x, as then the function would be undefined.
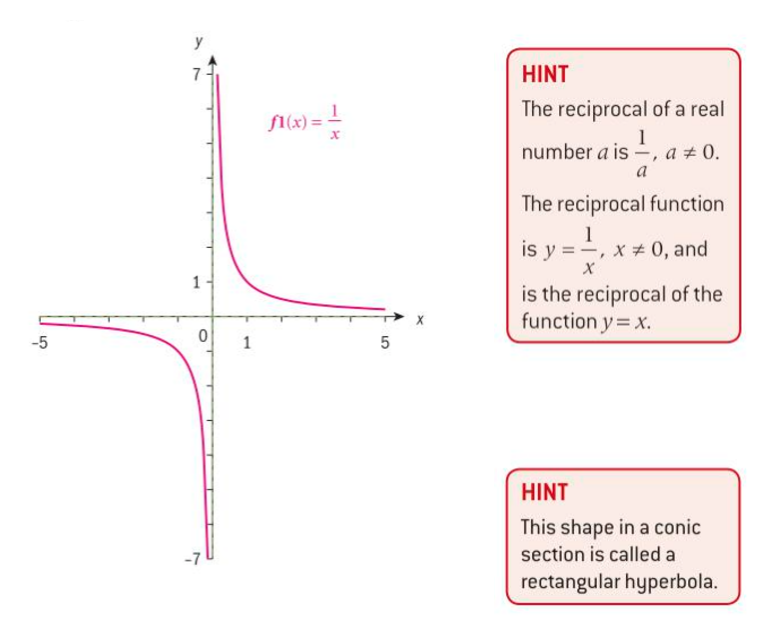



- Hyperbolas have a unique trait, which is that they are actually mirrored along the line f(x) = -x!
Piecewise Functions
- You can think of piecewise functions as sort of "Frankenstein" functions made from stitching together the parts of different functions.
- Each function is given a certain domain for which it is drawn.
- In fact, some of the functions we've already seen can be defined as piecewise functions, such as the modulus function:

Due to the nature of piecewise functions, they might not necessarily be continuous.
They might have vertical gaps where there is a difference in one function ends and the other starts.
Sources
https://study.com/academy/lesson/how-to-graph-cubics-quartics-quintics-and-beyond.html