What is Quadratic Equation?
- A quadratic equation is any equation that has the term x².
- Generally they are formed through the equation (x+a)(x+b), where a and b are normal numbers.
- When expanding the brackets, we get the equation x² + (a+b)x +ab.
- When graphed, quadratic equations look like parabolas.
Solving Quadratics
Factorization
- When a quadratic equation can be expressed as the product of two linear factors, you can factorize the equation and solve it.



Completing the Square
- Most quadratic equations you will come across do not involve a perfect square.

- However, they can easily be transformed into an expression which does involve a perfect square through completing the square.
- It is not always possible to factorize a quadratic equation. Completing the square is another method that can be used to solve quadratic equations.
- This method works as long as the equation as real solutions.
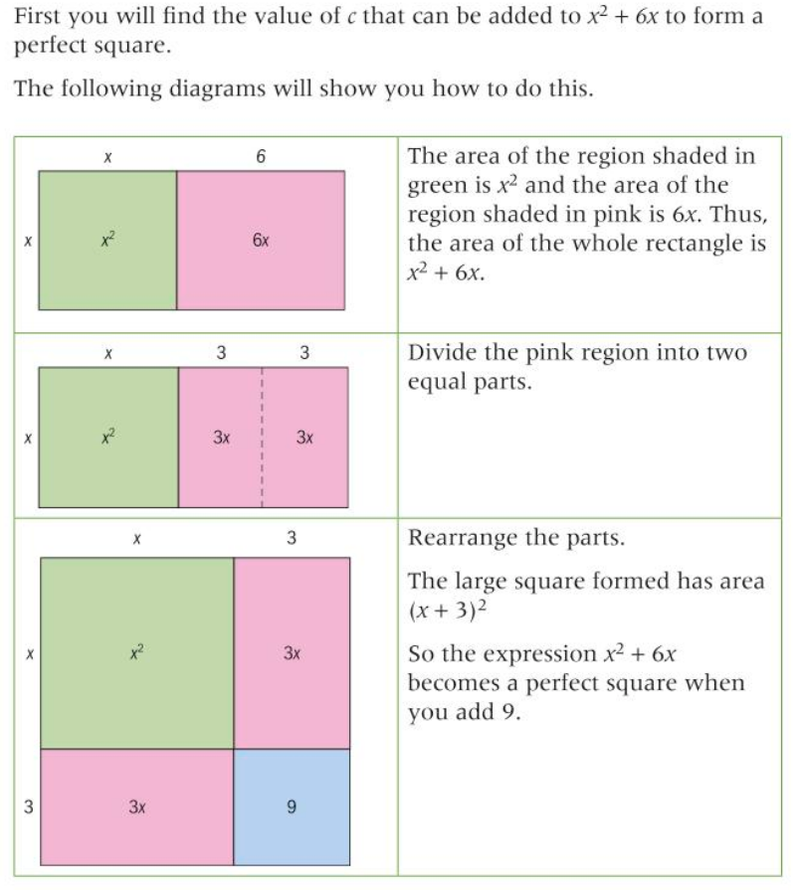
- So to complete the square, we find out that we were missing 9.
- Thus x² + 6x = 0 can be factorized into (x +3)² = 9 as 9 is added to both sides.
The Quadratic Formula
- You can generally solve a quadratic equation by factorization when its roots are integers, but you can always sole a quadratic equation by completing the square, even if the roots are surds.
- However, the disadvantage of completing the square is that it can be long and repetitive.
- The quadratic formula is a condensed way of using the completing the square method.

- It works for any quadratic equation with real roots.
- When either the coefficients b and/or c are equal to zero, we have special cases that can be solved more simply.

Discriminant of a Quadratic Equation
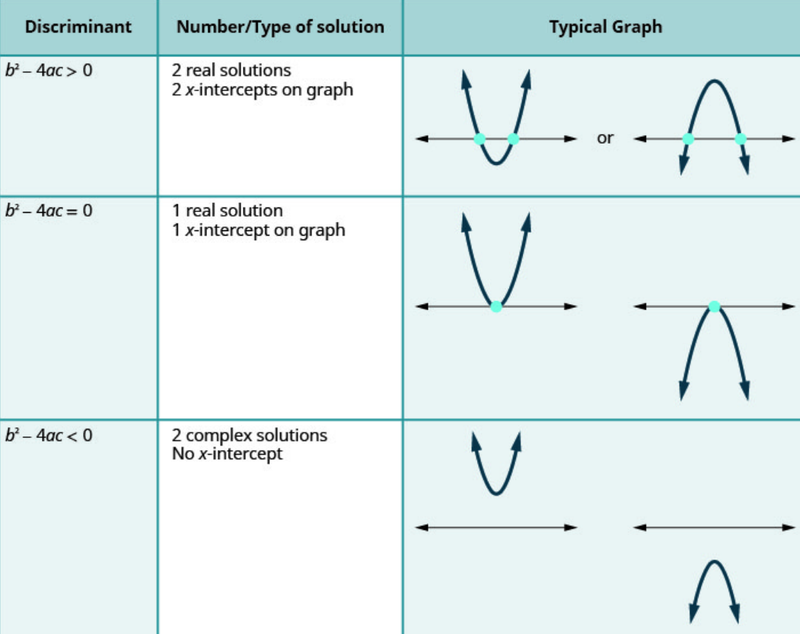
- Every quadratic equation has a discriminant, that determines the output of the quadratic.
- It is the area under the square root of the quadratic formula.

- The discriminant also correlates with the graph of a quadratic equation.
- When Δ > 0, then the parabola's vertex is below the x-axis and it has 2 roots
- When Δ = 0, the parabola is touching the x-axis and has one root.
- When Δ < 0, the parabola is above the x-axis and has no roots.
- These are the opposite for a negative parabola, which is flipped relative to the x-axis.
Sources
https://www.youtube.com/watch?v=52STqk6vrYM
https://pressbooks.bccampus.ca/algebraintermediate/chapter/solve-quadratic-inequalities/