Classification of Functions
One-To-One and Many-To-One Functions

- One to one functions are also called surjective functions, and many to one functions are called injective functions.
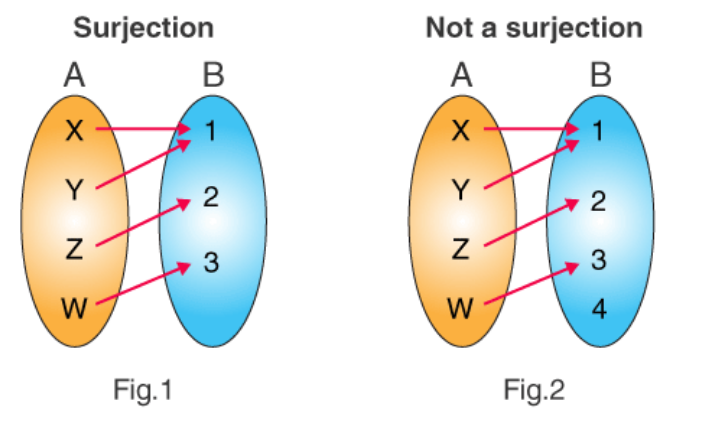
- An onto, or surjective function is a one-to-one function that maps every value in the domain to a value in the range.
- If there are certain values of y that are not mapped, it means that the function is not onto.
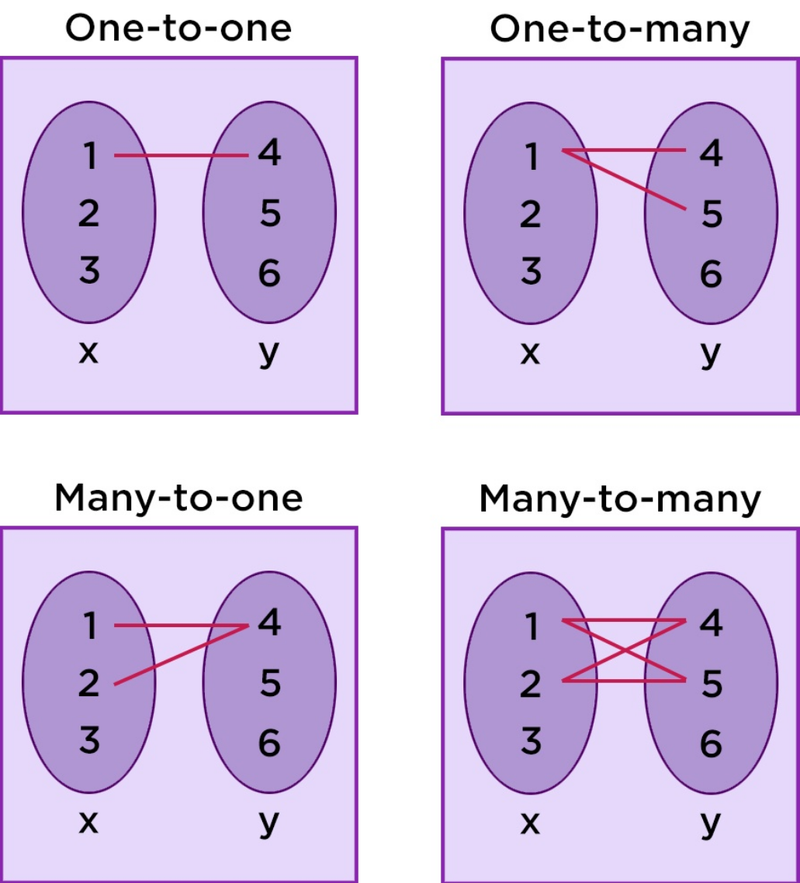
- One-to-many and many-to-many mapping are not functions but relations.
- If a horizontal line crosses only one point on a function, then it is surjective.
- If a horizontal line crosses more than one point on a function, then it is injective.
- If a vertical line crosses more than one point on a graph, then it is a relation.
Odd and Even Functions


- Functions can also be neither odd or even.
Function Composition
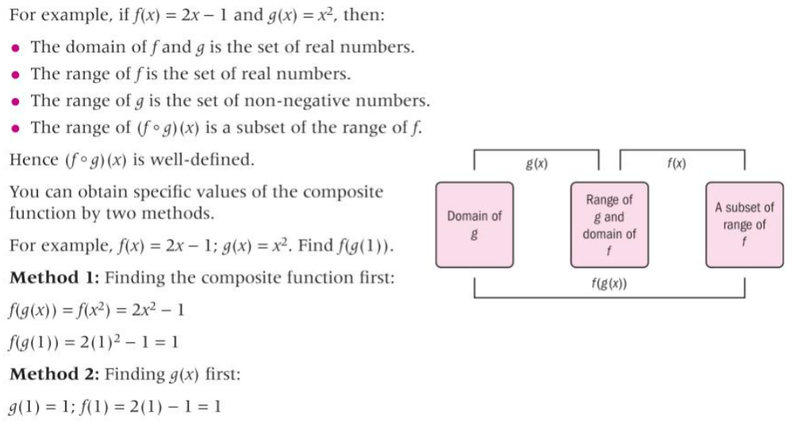
- Another operation that combines two functions to form a new function is function composition.
- In this operation the output of one function becomes the input of another function.

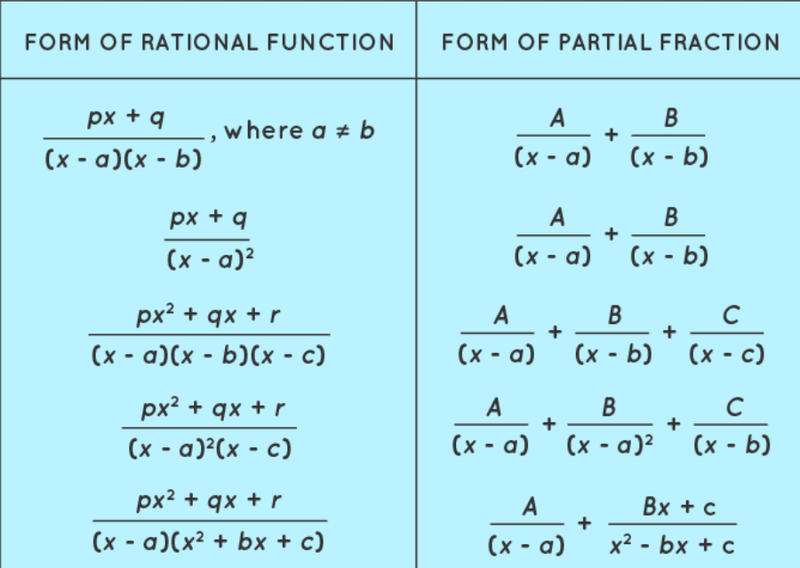
Partial Fraction Decomposition
- Larger functions can be very complicated.
- However, they can be made simpler by splitting them up into smaller functions.
- For rational functions, you can split up their denominators to obtain a different function.

- This works even if the numerator is a more complicated value such as an equation, as long as you can solve for A and B.
Identity Function

Inverse Function

- If two functions are inverses of each other, their graphs have a reflection symmetry about the line y = x.
- Only functions that are one to one and onto have inverse functions.
- We say that the functions have a one-to-one correspondence.
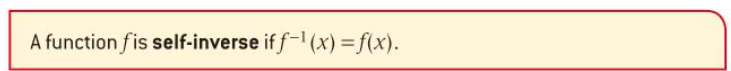
- For example the function 1/x is self-inverse.
Sources
https://www.expii.com/t/when-is-a-relation-a-function-4325