Permutations and Combinations

Permutations

• A permutation is the number of ways distinct objects can be arranged in a distinct order in a specific set.
• In permutation order does matter.

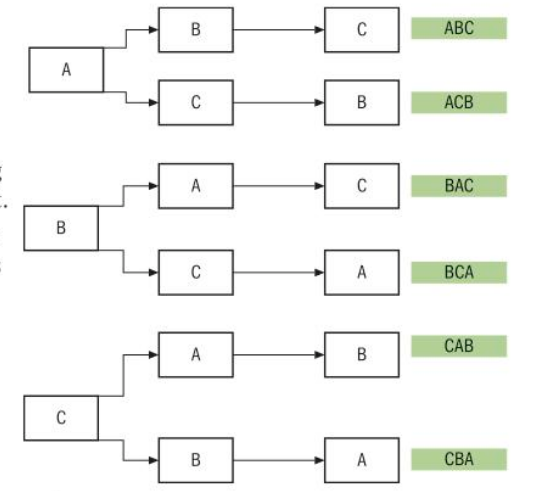
• Suppose you want to find the total number of arrangements of the three letters A, B and C.
• If you first chose A, then you can pick between B and C.
• If you pick A, then B, then your only option is C.
• However, if you pick C first, then your options are A and B, and the order is different.
• The total number of ways you can arrange A, B and C is the factorial of the amount of options, which is 3.
• So you can arrange A, B and C in 3! = 6 ways.

• Now imagine you have 5 letters, A, B, C, D and E.
• But you can still arrange only 3 letters together, and have to leave two of them out.
• All the possible combinations are given by the permutation.

Combinations

• Combinations are similar to permutations, except the order doesn't matter.
• For example, for arranging the letters A, B and C, there is only one possible combination, even though there are 6 possible permutations.
• This is because in a combination ABC, CBA, CAB, etc. are not considered distinct, while they are distinct in a permutation.
• A combination is given by: