What is Euler's Number?
- Euler's number, written as e, is an irrational number that is roughly equal to 2.718.
- As it is irrational, the decimal goes on forever, like π.
- It is very important in mathematics and is often used in natural logarithms, exponential functions and continuous compound interest.
Where Does e Come from?
- Just like how π is obtained by dividing a circle's circumference by its diameter, Euler's number is also obtained in a specific way.
- It comes from the formula:
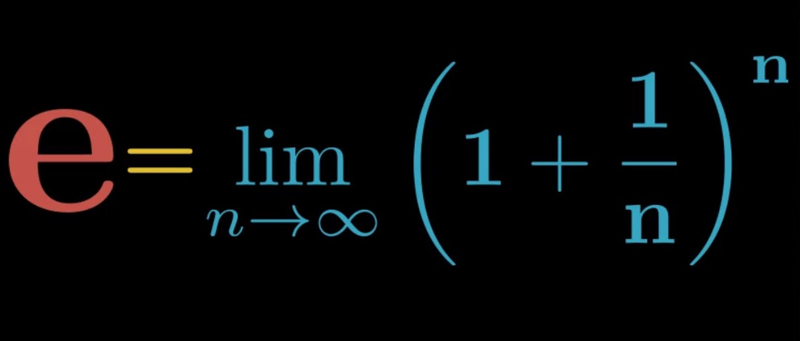
- As n gets bigger and bigger, the result of this equation gets closer and closer to Euler's number.
- This can be seen on the graph for the function.
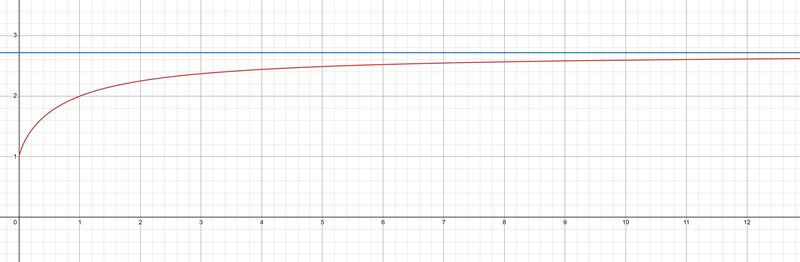
- The blue line is e and the red line is the graph of (1+1/n)ⁿ.
- e was originally calculated using the reciprocal of increasing factorials:

Special Properties of e
- e has some special properties, especially when it comes to derivatives and integrals.
- The derivative of eˣ is eˣ!
- This means that the gradient of the curve eˣ at any x value is the same as its y value at that x value.
- Likewise, the integral of eˣ is also eˣ!
- This means that the area under the graph eˣ at any x value is the same as the y value at that x value.
Cut Up Then Multiply Method
- Another way to get e is the "cut up and multiply method".
- Where you cut up a number into identical parts and then multiply them together to try and get the biggest product possible.
- For example for 8, we can see that the product is greatest when it is split into numbers that are closest to e.

Sources
https://www.youtube.com/watch?v=1kv0gjTHsYY
https://www.youtube.com/watch?v=BJp1VoCjAvo