What are Complex Numbers?
- To understand a complex number, we first need to understand what an imaginary number is.
- An imaginary number, as evidenced by its name, is not real, and is given as a square root with a radicant -1.
- An imaginary number is best imagined as a variable, just like x or y.
- Despite being imaginary, imaginary numbers have a lot of real-world applications!

- Complex numbers can be written in different forms.
- The form z = a + ib is called the Cartesian form of a complex number.
Geometric Approach
- A geometric approach can help us visualize complex numbers.
- We're used to visualizing real numbers on a number line, where each point on the line represents a real number.
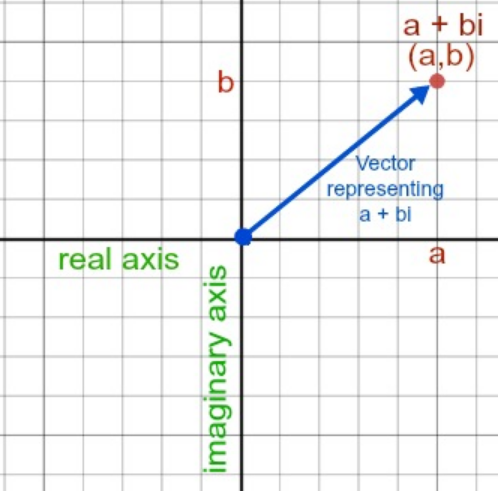
- In a similar way, complex numbers can be represented in a two-dimensional coordinate plane.
- In this case the horizontal axis is the real number line, but the vertical axis is the imaginary number line!
- Real numbers are still a point on the real number line, but complex numbers are a point anywhere on the coordinate plane!
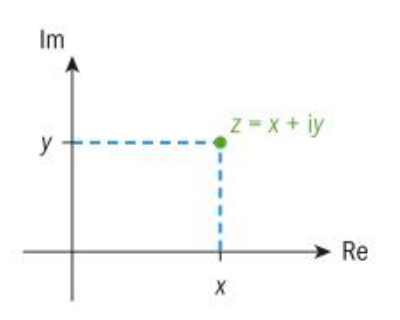
- Each complex number z = x + iy, where x and y are real numbers can be represented as a point P(x,y) one the plane.
- Like how purely real numbers lie on the horizontal axis, purely imaginary numbers lie on the vertical axis.
Modulus or Absolute Value of a Complex Number
- We already know that the modulus or absolute value of a real number is algebraically defined as:
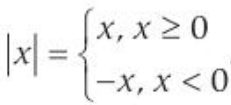
- Geometrically, the modulus represents the distance of a number from zero on a number line.
- This idea can be extended into two dimensions in the complex plane where the modulus of a complex number represents the distance between the complex number and the origin.
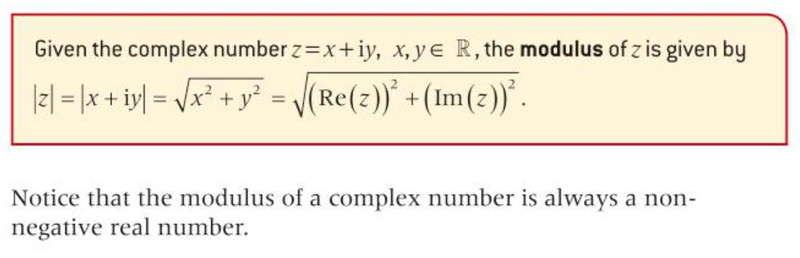
Operations with Complex Numbers
- When it comes to complex numbers, calculations aren't actually as complex as you think they might be!
- It helps to think of the imaginary and real parts completely separately.

- Both imaginary and real sides need to be equal. You cannot compensate for one side with the other as they are treated separately.
- When adding complex numbers or multiplying them by a constant, we use the following rules:
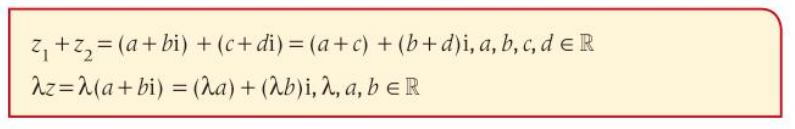
Multiplying Complex Numbers Together
- Remember how the imaginary number i =√-1.
- Any root to the power of two is equal to the radicand of the root.
- Therefore, i*i = -1!
- With this established, we can calculate the products of complex numbers as:
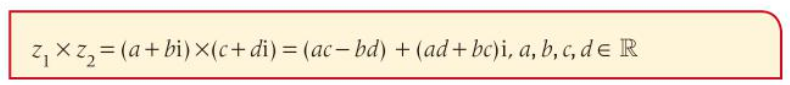
Conjugate Complex Numbers
- Conjugate complex numbers are a handy tool in operations with complex numbers.

- A complex number multiplied to its conjugate is equal to its modulus squared.
- This means that the complex number multiplied by its conjugate is a real number.
Division of Complex Numbers

- As the denominator is now equal to a real number, we can do the division!
Powers of Complex Numbers
- We discussed how i² = -1, but what about greater powers?
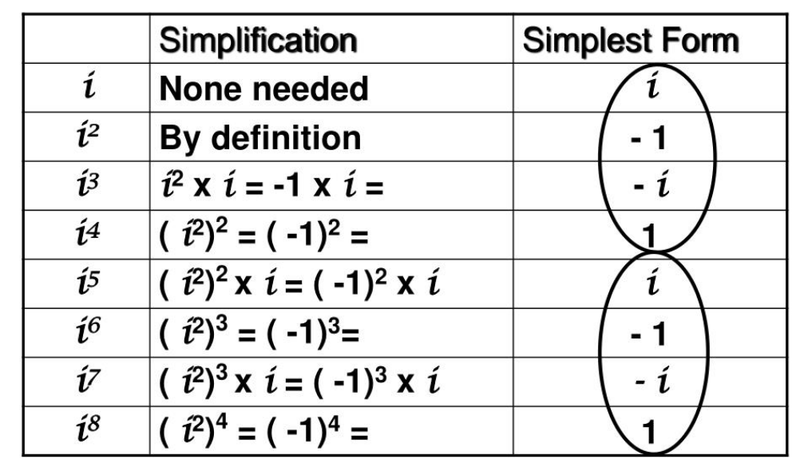
- From this chart we can see that all powers of i follow a certain pattern.
- Powers that are multiples of 2 result in -1, whereas multiples of 4 result in 1.
- Powers that are multiples of 1 result in i, and multiples of 3 result in -i.
- For complex numbers brought to higher powers, we can use the binomial theorem!
Roots of Complex Numbers



Sources
https://study.com/academy/lesson/representing-complex-numbers-with-vectors.html